题目内容
正四面体ABCD的外接球的表面积为4π,则A与B两点的球面距离为( )
A.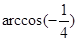 | B.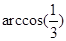 |
C.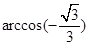 | D.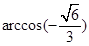 |
B
解:半径为1的球面上的四点A,B,C,D是正四面体的顶点,
所以正四面体扩展为正方体的外接球与圆柱球相同,
正方体的对角线就是外接球的直径,
所以正四面体的棱长为: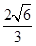
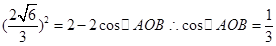
所以A与B两点的球面距离为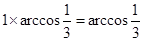
所以正四面体扩展为正方体的外接球与圆柱球相同,
正方体的对角线就是外接球的直径,
所以正四面体的棱长为:
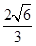
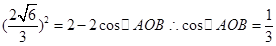
所以A与B两点的球面距离为

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
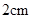 的圆柱器皿中(底面水平放置),量得水面的高度为
的圆柱器皿中(底面水平放置),量得水面的高度为 .若将这些水倒入轴截面是正三角形的倒置的圆锥形器皿中,则水面的高度是( )
.若将这些水倒入轴截面是正三角形的倒置的圆锥形器皿中,则水面的高度是( )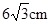
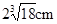
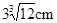
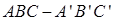 中,
中,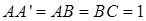 ,
, .棱
.棱 上有两个动点E,F,且EF = a (a为常数).
上有两个动点E,F,且EF = a (a为常数).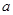
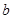
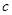
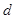
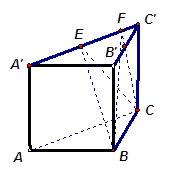
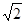 ,则球O的表面积为( )
,则球O的表面积为( )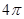 B、
B、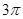 C、
C、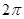 D、
D、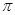
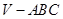 中,
中,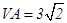 ,
,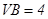 ,
,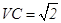 ,点
,点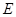 为侧棱
为侧棱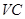 上的一点,
上的一点,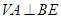 ,且顶点
,且顶点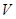 在底面
在底面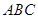 上的射影为底面的垂心.如果球
上的射影为底面的垂心.如果球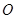 是三棱锥
是三棱锥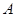 两点的球面距离是( )
两点的球面距离是( )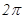
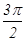
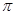
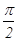
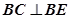 ;
;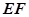 与平面
与平面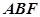 所成角的正弦值.
所成角的正弦值.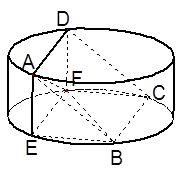
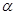 :A、B、C、D中有三个点到
:A、B、C、D中有三个点到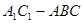 中,四边形
中,四边形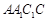 为平行四边形,且面
为平行四边形,且面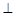 面
面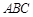 ,
,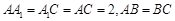 ,且
,且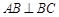 ,
,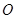 为
为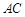 中点.
中点.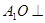 平面
平面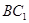 与底面
与底面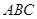 所成角的正弦值.
所成角的正弦值.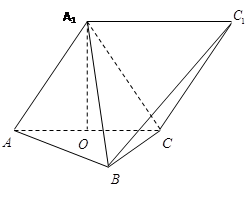
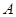 为端点的三条棱长都等于1,且它们彼此的夹角都是
为端点的三条棱长都等于1,且它们彼此的夹角都是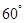 ,那么以这个顶点为端点的晶体的对角线的长为 。
,那么以这个顶点为端点的晶体的对角线的长为 。