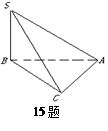
题目内容
如图,几何体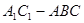 中,四边形
中,四边形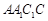 为平行四边形,且面
为平行四边形,且面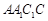
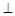 面
面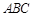 ,
,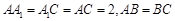 ,且
,且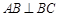 ,
,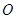 为
为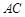 中点.
中点.
(Ⅰ)证明: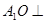 平面
平面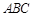 ;
;
(Ⅱ)求直线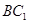 与底面
与底面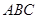 所成角的正弦值.
所成角的正弦值.
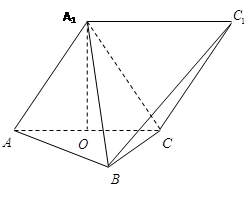
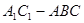 中,四边形
中,四边形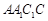 为平行四边形,且面
为平行四边形,且面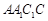
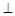 面
面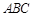 ,
,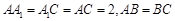 ,且
,且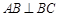 ,
,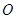 为
为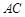 中点.
中点.(Ⅰ)证明:
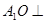 平面
平面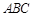 ;
;(Ⅱ)求直线
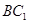 与底面
与底面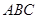 所成角的正弦值.
所成角的正弦值.
解:(Ⅰ)证明:因为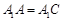 ,且O为AC的中点,所以
,且O为AC的中点,所以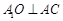 .
.
又由题意可知,平面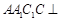 平面
平面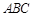 ,交线为
,交线为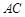 ,且
,且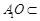 平面
平面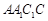 ,
,
所以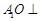 平面
平面 . ……..(5分)
. ……..(5分)
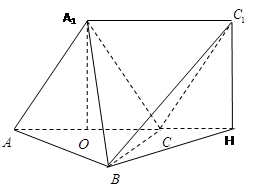
(Ⅱ)如图,过 作
作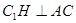 ,交
,交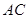 的延长线于
的延长线于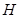 .因为
.因为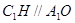 ,则
,则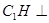 底面
底面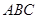 ,连
,连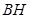 ,所以
,所以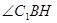 就是直线
就是直线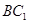 与底面
与底面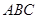 所成角.又因为
所成角.又因为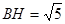 ,
,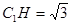 ,所以
,所以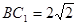 .所以
.所以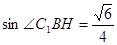 . ….. …….. …....(10分)
. ….. …….. …....(10分)
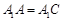 ,且O为AC的中点,所以
,且O为AC的中点,所以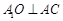 .
. 又由题意可知,平面
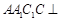 平面
平面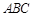 ,交线为
,交线为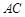 ,且
,且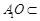 平面
平面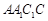 ,
, 所以
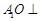 平面
平面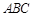 . ……..(5分)
. ……..(5分) 
(Ⅱ)如图,过
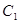 作
作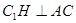 ,交
,交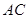 的延长线于
的延长线于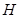 .因为
.因为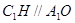 ,则
,则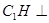 底面
底面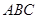 ,连
,连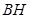 ,所以
,所以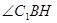 就是直线
就是直线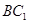 与底面
与底面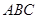 所成角.又因为
所成角.又因为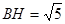 ,
,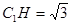 ,所以
,所以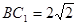 .所以
.所以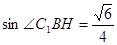 . ….. …….. …....(10分)
. ….. …….. …....(10分) 略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
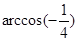
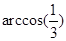
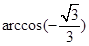
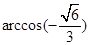
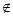 直线l , 则由点P和直线l确定的平面的个数是
直线l , 则由点P和直线l确定的平面的个数是 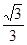
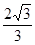
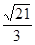
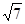
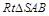 的两边
的两边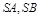 互相垂直,且
互相垂直,且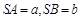 ,则
,则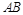 边上的高
边上的高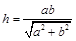 ;现在把结论类比到空间:三棱锥
;现在把结论类比到空间:三棱锥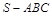 的三条侧棱
的三条侧棱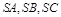 两两相互垂直,
两两相互垂直,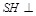 平面
平面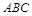 ,且
,且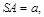
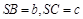 ,则点
,则点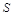 到平面
到平面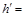
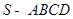 的侧棱长为
的侧棱长为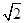 ,底面边长为
,底面边长为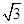 ,
,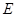 为
为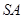 中点,则异面直线
中点,则异面直线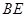 与
与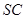 所成的角是( )
所成的角是( )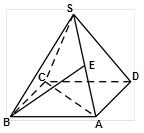
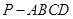 中,
中,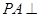 底面
底面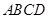 ,
,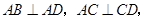
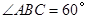 ,
,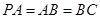 ,
,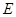 是
是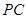 的中点.
的中点.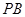 和平面
和平面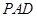 所成的角的大小;
所成的角的大小;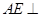 平面
平面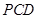 ;
;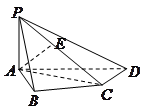
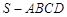 ,底面四边形ABCD满足条件
,底面四边形ABCD满足条件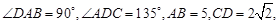 ,
,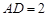 ,侧面SAD垂直于底面ABCD,
,侧面SAD垂直于底面ABCD,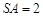 ,
,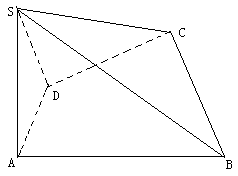
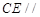 平面SAD,求
平面SAD,求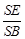 的值;
的值;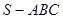 中,
中, 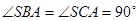 , △
, △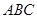 是斜边
是斜边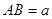 的等腰直角三角形, 则以下结论中: ① 异面直线
的等腰直角三角形, 则以下结论中: ① 异面直线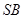 与
与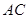 所成的角为
所成的角为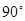 ; ② 直线
; ② 直线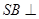 平面
平面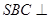 面
面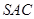 ; ④ 点
; ④ 点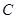 到平面
到平面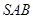 的距离是
的距离是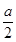 . 其中正确结论的序号是 ______
. 其中正确结论的序号是 ______