题目内容
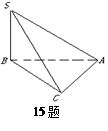
空间给定不共面的A、B、C、D四个点,其中任意两点的距离都不相同,考虑具有如下性质的平面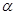 :A、B、C、D中有三个点到
:A、B、C、D中有三个点到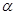 的距离相同,另外一个点到
的距离相同,另外一个点到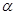 的距离是前三个点到
的距离是前三个点到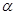 的距离的2倍,这样的平面的个数是
的距离的2倍,这样的平面的个数是
A.15 B.23 C.26 D.32
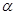 :A、B、C、D中有三个点到
:A、B、C、D中有三个点到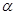 的距离相同,另外一个点到
的距离相同,另外一个点到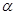 的距离是前三个点到
的距离是前三个点到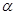 的距离的2倍,这样的平面的个数是
的距离的2倍,这样的平面的个数是 A.15 B.23 C.26 D.32
D
首先取3个点相等,不相等的那个点有四种取法。
3个点距离相等,有两种可能性:
(1)全同侧。这样的平面有两个;
(2)不同侧,必然2个点在一侧,另个点在一侧分,1个点的取法有3种,并且平面过三角形两个点边上的中位线。考虑不相等的点与单侧点是否同侧有两种可能,每种情况下都唯一确定一个平面。有6个。
所以最后有8个。答案应该是32.
3个点距离相等,有两种可能性:
(1)全同侧。这样的平面有两个;
(2)不同侧,必然2个点在一侧,另个点在一侧分,1个点的取法有3种,并且平面过三角形两个点边上的中位线。考虑不相等的点与单侧点是否同侧有两种可能,每种情况下都唯一确定一个平面。有6个。
所以最后有8个。答案应该是32.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
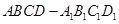 是正方体,点
是正方体,点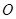 为正方体对角线的交点,过点
为正方体对角线的交点,过点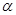 ,正方体的八个顶点到平面
,正方体的八个顶点到平面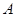 的元素,则集合
的元素,则集合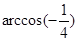
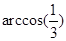
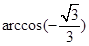
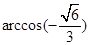
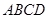 与
与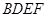 均为菱形,
均为菱形,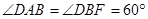 ,且
,且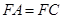 .
.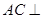 平面
平面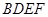 ;
;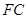 ∥平面
∥平面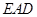 ;
;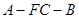 的余弦值.
的余弦值.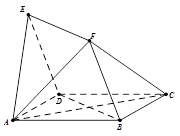
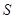 是
是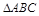 所在平面外的一点,且
所在平面外的一点,且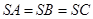 ,若
,若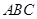 内的射影落在
内的射影落在 ABC外部,则
ABC外部,则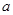 的正方体的各顶点都在半径为R的球面上,则
的正方体的各顶点都在半径为R的球面上,则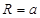
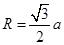
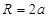
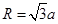
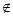 直线l , 则由点P和直线l确定的平面的个数是
直线l , 则由点P和直线l确定的平面的个数是 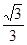
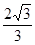
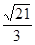
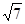
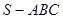 中,
中, 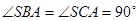 , △
, △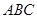 是斜边
是斜边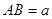 的等腰直角三角形, 则以下结论中: ① 异面直线
的等腰直角三角形, 则以下结论中: ① 异面直线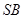 与
与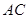 所成的角为
所成的角为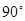 ; ② 直线
; ② 直线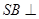 平面
平面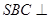 面
面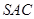 ; ④ 点
; ④ 点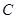 到平面
到平面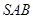 的距离是
的距离是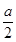 . 其中正确结论的序号是 ______
. 其中正确结论的序号是 ______