题目内容
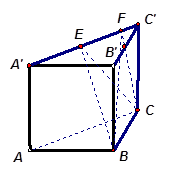
如图,在直三棱柱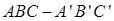 中,
中,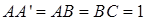 ,
,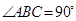 .棱
.棱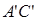 上有两个动点E,F,且EF = a (a为常数).
上有两个动点E,F,且EF = a (a为常数).
(Ⅰ)在平面ABC内确定一条直线,使该直线与直线CE垂直;
(Ⅱ)判断三棱锥B—CEF的体积是否为定值.若是定值,求出这个三棱锥的体积;若不是定值,说明理由.
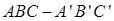 中,
中,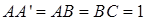 ,
,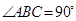 .棱
.棱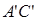 上有两个动点E,F,且EF = a (a为常数).
上有两个动点E,F,且EF = a (a为常数).(Ⅰ)在平面ABC内确定一条直线,使该直线与直线CE垂直;
(Ⅱ)判断三棱锥B—CEF的体积是否为定值.若是定值,求出这个三棱锥的体积;若不是定值,说明理由.
| * | 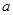 | 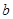 | 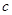 | 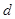 |
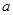 | 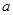 | 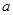 |  |  |
 |  |  |  |  |
 | 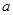 | 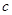 | 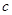 | 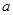 |
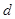 | 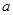 | 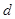 | 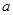 | 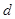 |

(Ⅰ)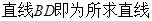 .(Ⅱ)
.(Ⅱ)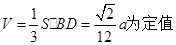
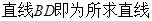 .(Ⅱ)
.(Ⅱ)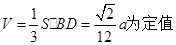
本试题主要考查了立体几何中点线面的位置关系的运用。
解: (Ⅰ)取AC中点D,连接BD.
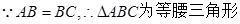 ,D为底边AC中点,∴
,D为底边AC中点,∴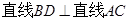 .
.
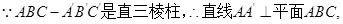
∵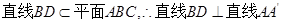 .
.
又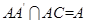 ,∴直线
,∴直线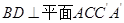 .∵
.∵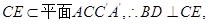
∴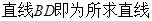 . --5分
. --5分
(Ⅱ)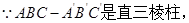 直线
直线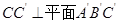 ,
,
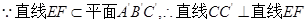 .
.
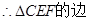 EF上的高为线段
EF上的高为线段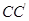 ,由已知条件得
,由已知条件得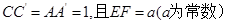 ,
,
故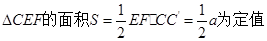
由(Ⅰ)可知,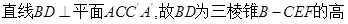 .
.
在等腰三角形ABC中,可求得BD=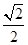 ,
,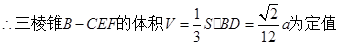
解: (Ⅰ)取AC中点D,连接BD.
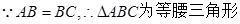 ,D为底边AC中点,∴
,D为底边AC中点,∴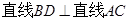 .
.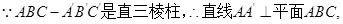
∵
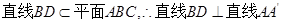 .
.又
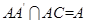 ,∴直线
,∴直线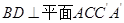 .∵
.∵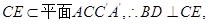
∴
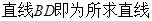 . --5分
. --5分(Ⅱ)
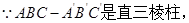 直线
直线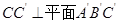 ,
,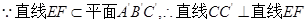 .
.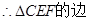 EF上的高为线段
EF上的高为线段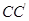 ,由已知条件得
,由已知条件得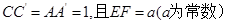 ,
,故
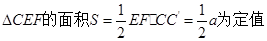
由(Ⅰ)可知,
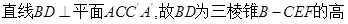 .
.在等腰三角形ABC中,可求得BD=
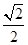 ,
,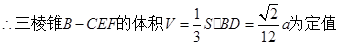

练习册系列答案
相关题目
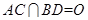 ,
,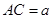 ,得到三棱锥
,得到三棱锥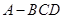 ,如图所示。
,如图所示。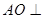 平面BCD;
平面BCD;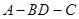 的大小为
的大小为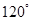 时,
时,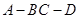 的正切值。
的正切值。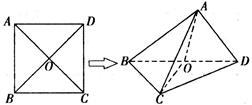
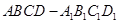 中,
中,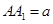 ,
,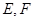 分别是
分别是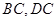 的中点,则异面直线
的中点,则异面直线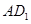 与
与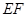 所成角为
所成角为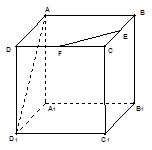
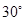
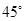
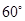
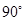
 中,侧棱垂直底面,∠ACB=90°,AC=BC=AA1,D是棱AA1的中点。
中,侧棱垂直底面,∠ACB=90°,AC=BC=AA1,D是棱AA1的中点。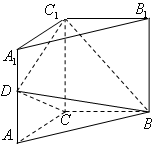
 ⊥平面
⊥平面 是正方体,点
是正方体,点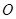 为正方体对角线的交点,过点
为正方体对角线的交点,过点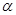 ,正方体的八个顶点到平面
,正方体的八个顶点到平面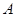 的元素,则集合
的元素,则集合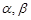 为两个不重合的平面,
为两个不重合的平面,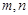 是两条不重合的直线,给出下列四个命题:
是两条不重合的直线,给出下列四个命题: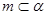 ,
,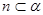 ,
,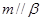 ,
,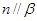 ,则
,则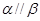 ;②若
;②若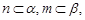
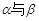 相交且不垂直,则
相交且不垂直,则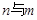 不垂直;③若
不垂直;③若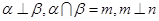 ,则n⊥
,则n⊥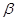 ; ④若
; ④若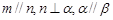 ,则
,则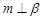 .其中所有真命题的序号是 .
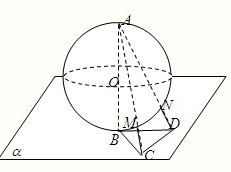
.其中所有真命题的序号是 .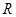 的球
的球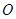 的直径
的直径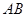 垂直于平面
垂直于平面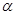 ,垂足为
,垂足为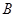 ,
,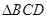 是平面
是平面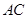 、
、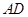 分别与球面交于点M,N,那么M、N两点间的球面距离是( )
分别与球面交于点M,N,那么M、N两点间的球面距离是( )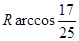
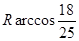
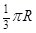
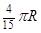
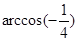
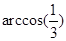
 直线l , 则由点P和直线l确定的平面的个数是
直线l , 则由点P和直线l确定的平面的个数是