题目内容
【题目】已知数列{an}的前n项和为Sn ， 且 
，数列{bn}满足 
，则数列{anbn}的前n项和Tn= ．
【答案】10+（3n﹣5）2n+1
【解析】解：由已知得，当n≥2时，an=Sn﹣Sn﹣1=（ 
n2﹣ 
n）﹣[ （n﹣1）2﹣ （n﹣1）]=3n﹣2，又a1=1=3×1﹣2，符合上式．
故数列{an}的通项公式an=3n﹣2．
又因为 
，
所以log2bn= 
（an+2）=n，即bn=2n ，
令cn=anbn ．
则cn=（3n﹣2）2n ．
所以Tn=1×21+422+723+…+（3n﹣2）2n ， ①
2Tn=1×22+4×23+724+…+（3n﹣2）2n+1 ， ②
由②﹣①得：﹣Tn=2+322+323+…+（3n﹣5）2n+1=3×（2+22+…+2n）﹣（3n﹣2）2n+1﹣2
=﹣（3n﹣5）2n+1﹣10，
所以Tn=10+（3n﹣5）2n+1
故答案是：10+（3n﹣5）2n+1 ．
【考点精析】本题主要考查了数列的前n项和的相关知识点，需要掌握数列{an}的前n项和sn与通项an的关系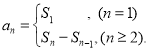
才能正确解答此题．
练习册系列答案
相关题目
