题目内容
已知抛物线方程为y2=4x,直线l的方程为x-y+4=0,在抛物线上有一动点P到y轴的距离为d1,P到直线l的距离为d2,则d1+d2的最小值为( )
A.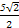 +2 +2 | B.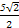 +1 +1 | C.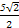 -2 -2 | D.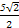 -1 -1 |
D
【思路点拨】画出图象,通过图象可知点P到y轴的距离等于点P到焦点F的距离减1,过焦点F作直线l的垂线,此时d1+d2最小,根据抛物线方程求得F的坐标,进而利用点到直线的距离公式求得d1+d2的最小值.
如图所示,
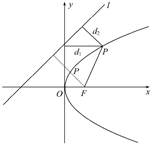
由抛物线的定义知,|PF|=d1+1,
∴d1=|PF|-1,
d1+d2=d2+|PF|-1,显然当直线PF垂直于直线x-y+4=0时,d1+d2最小,此时d2+|PF|为F到直线x-y+4=0的距离.
由题意知F点的坐标为(1,0),
所以(d2+|PF|)min=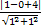 =
=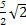 .
.
∴(d1+d2)min=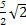 -1.
-1.
如图所示,

由抛物线的定义知,|PF|=d1+1,
∴d1=|PF|-1,
d1+d2=d2+|PF|-1,显然当直线PF垂直于直线x-y+4=0时,d1+d2最小,此时d2+|PF|为F到直线x-y+4=0的距离.
由题意知F点的坐标为(1,0),
所以(d2+|PF|)min=
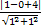 =
=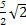 .
.∴(d1+d2)min=
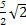 -1.
-1.
练习册系列答案
相关题目
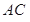 、
、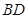 是过抛物线
是过抛物线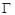 焦点
焦点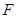 的两条弦,且其焦点
的两条弦,且其焦点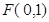 ,
,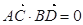 ,点
,点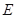 为
为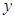 轴上一点,记
轴上一点,记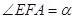 ,其中
,其中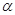 为锐角.
为锐角.
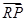 ·
·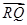 的最小值.
的最小值.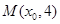 发出的光线,沿平行于抛物线
发出的光线,沿平行于抛物线 的对称轴方向射向此抛物线上的点
的对称轴方向射向此抛物线上的点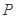 ,经抛物线反射后,穿过焦点射向抛物线上的点
,经抛物线反射后,穿过焦点射向抛物线上的点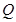 ,再经抛物线反射后射向直线
,再经抛物线反射后射向直线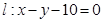 上的点
上的点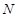 ,经直线反射后又回到点
,经直线反射后又回到点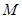 ,则
,则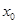 等于( )
等于( )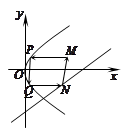




 ),C(x,y),若
),C(x,y),若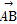 ⊥
⊥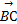 ,则动点C的轨迹方程是_________.
,则动点C的轨迹方程是_________. x2上一点,F为抛物线的焦点.A在C:(x-1)2+(y-4)2=1上,则|MA|+|MF|的最小值为( )
x2上一点,F为抛物线的焦点.A在C:(x-1)2+(y-4)2=1上,则|MA|+|MF|的最小值为( )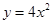 上的一点
上的一点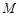 到焦点的距离为1,则点
到焦点的距离为1,则点