题目内容
12.如果角α的终边过点(2sin$\frac{π}{6}$,-2cos$\frac{π}{6}$),则sinα的值等于( )| A. | $\frac{\sqrt{2}}{2}$ | B. | -$\frac{1}{2}$ | C. | -$\frac{\sqrt{2}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
分析 根据三角函数的坐标法定义,首先求出到原点的距离,得到sinα.
解答 解:因为角α的终边过点(2sin$\frac{π}{6}$,-2cos$\frac{π}{6}$),即为(1,-$\sqrt{3}$),因为此点到原点的距离为2,所以sinα=$-\frac{\sqrt{3}}{2}$;
故选D.
点评 本题考查了三角函数的坐标法定义;关键是明确利用角的终边上的点表示三角函数.

练习册系列答案
相关题目
17.从001,002,…,500这500个号中用系统抽样的方法抽取一个容量为10的样本,已知样本中最小编号为015,从样本随机抽出3个号,至少有两个数被3整除的抽法有( )种.
| A. | 60 | B. | 40 | C. | 120 | D. | 36 |
4.向量$\overrightarrow a$=(2,0),$\overrightarrow b$=(x,y),若$\overrightarrow b$与$\overrightarrow b$-$\overrightarrow a$的夹角为30°,则$|{\overrightarrow b}|$的最大值为( )
| A. | 2 | B. | 2$\sqrt{3}$ | C. | 4 | D. | $\frac{{4\sqrt{3}}}{3}$ |
1.若f(x)=sinx+cosx,f′(x)是f(x)的导函数,要得到g(x)=$\sqrt{2}f(x){f}^{′}$(x)的图象,需将f(2x)的图象( )
| A. | 向左平移$\frac{π}{8}$个单位 | B. | 向右平移 $\frac{π}{8}$个单位 | ||
| C. | 向左平移$\frac{π}{4}$个单位 | D. | 向右平移$\frac{π}{4}$个单位 |
2.已知$\overrightarrow{a}$=(3,1),$\overrightarrow{b}$=(x,x-1)且$\overrightarrow{a}$∥$\overrightarrow{b}$,则x等于( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | 3 | D. | $\frac{3}{2}$ |
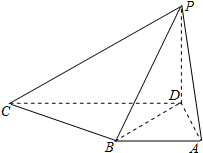 在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,AB∥CD,∠BAD=90°,AB=AD=1,CD=2.
在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,AB∥CD,∠BAD=90°,AB=AD=1,CD=2.