题目内容
11.已知双曲线$\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的一个焦点在直线y=2x-10上,则双曲线的方程为$\frac{{x}^{2}}{5}-\frac{{y}^{2}}{20}=1$.分析 可得双曲线的焦点在x轴,焦点为(5,0),故52=5+b2,可得b2=20,进而可得双曲线的方程.
解答 解:由题意可得双曲线的焦点在x轴,
故令y=0,代入y=2x-10可得x=5,
故其中的一个焦点为(5,0),可得52=5+b2,
解得b2=20,故可得双曲线的方程为$\frac{{x}^{2}}{5}-\frac{{y}^{2}}{20}=1$.
故答案为:$\frac{{x}^{2}}{5}-\frac{{y}^{2}}{20}=1$.
点评 本题考查双曲线的简单性质,涉及双曲线的焦点求解,属中档题.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
2.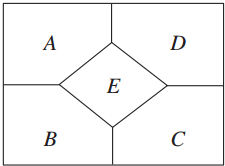 如图所示的五个区域中,现有四种颜色可供选择.要求每一个区域只涂一种颜色,相邻区域所涂颜色不同,则不同的涂色方法种数为( )
如图所示的五个区域中,现有四种颜色可供选择.要求每一个区域只涂一种颜色,相邻区域所涂颜色不同,则不同的涂色方法种数为( )
 如图所示的五个区域中,现有四种颜色可供选择.要求每一个区域只涂一种颜色,相邻区域所涂颜色不同,则不同的涂色方法种数为( )
如图所示的五个区域中,现有四种颜色可供选择.要求每一个区域只涂一种颜色,相邻区域所涂颜色不同,则不同的涂色方法种数为( )| A. | 24种 | B. | 48种 | C. | 72种 | D. | 96种 |
16.已知离心率为$\frac{1}{2}$的椭圆的左右焦点分别为F1,F2,椭圆上一点P满足:|PF1|=2|PF2|,则cos∠PF1F2=( )
| A. | $\frac{11}{16}$ | B. | $\frac{7}{8}$ | C. | -$\frac{1}{4}$ | D. | 不确定 |
4.向量$\overrightarrow a$=(2,0),$\overrightarrow b$=(x,y),若$\overrightarrow b$与$\overrightarrow b$-$\overrightarrow a$的夹角为30°,则$|{\overrightarrow b}|$的最大值为( )
| A. | 2 | B. | 2$\sqrt{3}$ | C. | 4 | D. | $\frac{{4\sqrt{3}}}{3}$ |
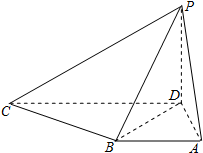 在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,AB∥CD,∠BAD=90°,AB=AD=1,CD=2.
在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,AB∥CD,∠BAD=90°,AB=AD=1,CD=2.