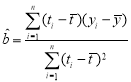题目内容
【题目】已知抛物线
：
上横坐标为4的点到焦点的距离为5.
（1）求抛物线的方程；
（2）设直线
与抛物线交于两点
、
，且
，
是弦
中点，过作平行于
轴的直线交抛物线于点
，得到
，再分别过弦
、
的中点作平行于轴的直线依次交抛物线于点
、
，得到
和
，按此方法继续下去，解决下列问题：
①求证：
；
②计算的面积
；
③根据的面积的计算结果，写出、的面积，请设计一种求抛物线与线段所围成封闭图形面积的方法，并求此封闭图形的面积.
【答案】（1）
；（2）①见解析； ②
；③
，无穷等比数列各项和.
.
【解析】
（1）由抛物线的定义、结合已知可以直接求出
的值，进而可以求出抛物线的方程；
（2）①：直线方程与抛物线方程联立，根据根的判别式、根与系数的关系、结合
，可以证明出
；
②：利用中点坐标公式和三角形面积公式直接求解即可；
③：同②可知：
只与有关，于是可知
，
分别与
、
有关，这样可以求出它们的面积；这样无限操作下去，每次得到的三角形面积都相等，面积是一个等比数列，每次得到的三角形的个数也是等比数列，利用无穷等比数列前
项和公式，这样可以求出抛物线
与线段
所围成封闭图形面积.
（1）抛物线的准线方程为：
，由抛物线的定义可知：
，所以抛物线的方程为：；
（2）①：联立直线和抛物线方程得：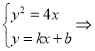
，
∴
，
；
∴
；
②：由中点坐标公式可得：
，∴
，
，
，
；
③：由同②可知：只与有关，而
，
所以
，这样无限操作下去，第次操作，得到
个小三角形，每个三角形的面积为：
，这无穷多个三角形的面积之和就是抛物线与线段所围成封闭图形面积，所以有
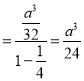
所求的面积为.
练习册系列答案
名题金卷系列答案
相关题目
