题目内容
15.设直线l经过点M0(1,5)、倾斜角为$\frac{π}{3}$.(1)求直线l的参数方程;
(2)若直线l和圆x2+y2=16的两个交点为A、B,求|MA|•|MB|.
分析 (1)由$k=tan\frac{π}{3}$=$\frac{sin\frac{π}{3}}{cos\frac{π}{3}}$,经过点M0(1,5),即可得出直线l的参数方程.
(2)把直线l的参数方程代入圆x2+y2=16可得${t}^{2}+(1+5\sqrt{3})t$+10=0.利用|MA|•|MB|=|t1t2|即可得出.
解答 解:(1)∵$k=tan\frac{π}{3}$=$\frac{sin\frac{π}{3}}{cos\frac{π}{3}}$,经过点M0(1,5),∴直线l的参数方程为$\left\{\begin{array}{l}{x=1+\frac{1}{2}t}\\{y=5+\frac{\sqrt{3}}{2}t}\end{array}\right.$.
(2)把直线l的参数方程代入圆x2+y2=16可得${t}^{2}+(1+5\sqrt{3})t$+10=0.
∴t1t2=10.
∴|MA|•|MB|=|t1t2|=10.
点评 本题考查了直线的参数方程及其应用、直线与曲线相交弦长问题,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
3.下列角的终边与37°角的终边在同一直线上的是( )
| A. | -37° | B. | 143° | C. | 379° | D. | -143° |
7.天文学家经研究认为:“地球和火星在太阳系中各方面比较接近,而地球有生命,进而认为火星上也有生命存在”,这是什么推理( )
| A. | 归纳推理 | B. | 类比推理 | C. | 演绎推理 | D. | 反证法 |
4.过点(5,3)且与直线x-2y-2=0垂直的直线方程是( )
| A. | x+2y-11=0 | B. | 2x+y-13=0 | C. | 2x-y-7=0 | D. | x-2y+1=0 |
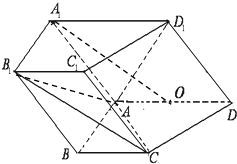 如图,在四棱柱ABCD-A1B1C1D1中,侧面A1ADD1⊥底面ABCD,D1A=D1D=$\sqrt{2}$,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
如图,在四棱柱ABCD-A1B1C1D1中,侧面A1ADD1⊥底面ABCD,D1A=D1D=$\sqrt{2}$,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.