题目内容
3.(-$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i)24的偶数项的和为0.分析 (-$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i)24的偶数项的和为,即复数(-$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i)24的虚部乘以i.再利用复数三角形式的乘方法则求得复数(-$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i)24的虚部,从而得出结论.
解答 解:(-$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i)24的偶数项的和为,即复数(-$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i)24的虚部乘以i.
由于(-$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i)24=${(cos\frac{2π}{3}+isin\frac{2π}{3})}^{24}$=cos16π+isin16π=1,故复数(-$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i)24的虚部为0,
故答案为:0.
点评 本题主要考查复数三角形式的乘方法则应用,体现了转化的数学思想,属于中档题.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
13.若点(1,1)在圆(x-a)2+(y+a)2=4的外部,那么a的取值范围是( )
| A. | (-1,1) | B. | (0,1) | C. | (-∞,-1)∪(1,+∞) | D. | {-1,1} |
14.集合A={x|0<x≤2},B={M|M⊆A},则A与B之间的关系为( )
| A. | A∈B | B. | A?B | C. | B∈A | D. | B?A |
18.若三角形周长为l,内切圆半径为r,则三角形的面积为s=$\frac{1}{2}$lr,根据类比思想,若四面体的表面积为S,内切球半径为R,则这个四面体的体积为V=$\frac{1}{3}$SR.
13.将函数y=sin2x的图象向左平移$\frac{π}{6}$,然后把所有图象上各点的横坐标伸长到原来的2倍,所得图象的解析式为( )
| A. | y=sin(x+$\frac{π}{6}$) | B. | y=sin(x+$\frac{π}{3}$) | C. | y=sin(4x+$\frac{π}{6}$) | D. | y=sin(4x+$\frac{π}{3}$) |
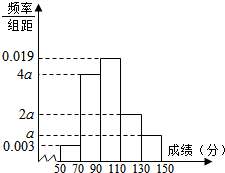 某高中组织50人参加自主招生选拔考试,其数学科测试全部成绩介于50分与150分之间(无满分),将测试结果按如下方式分成五组:第一组[50,70);第二组[70,90);…,第五组[130,150).下图为按上述分组方法得到的频率分布直方图.
某高中组织50人参加自主招生选拔考试,其数学科测试全部成绩介于50分与150分之间(无满分),将测试结果按如下方式分成五组:第一组[50,70);第二组[70,90);…,第五组[130,150).下图为按上述分组方法得到的频率分布直方图.