题目内容
【题目】已知椭圆C：
（a＞b＞0）的焦距为2，且过点
.
（1）求椭圆C的方程；
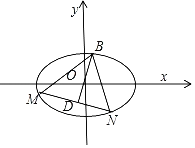
（2）已知△BMN是椭圆C的内接三角形，若坐标原点O为△BMN的重心，求点O到直线MN距离的最小值.
【答案】（1）
（2）
【解析】
（1）由题意焦距的值可得c的值，再由椭圆过点
，及a，b，c之间的关系求出a，b的值，进而求出椭圆的方程；
（2）分B的纵坐标为0和不为0两种情况讨论，设B的坐标，由O是三角形的重心可得MN的中点的坐标，设M，N的坐标，代入椭圆方程两式相减可得直线MN的斜率，求出直线MN的方程，求出O到直线MN的距离的表达式，再由B的纵坐标的范围求出d的取值范围，进而求出d的最小值.
解：（1）由题意可得：椭圆的焦距为2，则
，又椭圆过点
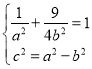，解得：a2＝4，b2＝3，
所以椭圆的方程为：
1；
（2）设B
，记线段MN中点D，
因为O为
BMN的重心，所以
2
，则点D的坐标为：
，
若n＝0，则|m|＝2，此时直线MN与x轴垂直，
故原点O到直线MN的距离为
，即为1，
若n≠0，此时直线MN的斜率存在，
设M（x1，y1），N（x2，y2），则x1+x2＝﹣m，y1+y2＝﹣n，
又
1，
1，
两式相减
0，
可得：kMN
，
故直线MN的方程为：y
（x
）
，即6mx+8ny+3m2+4n2＝0，
则点O到直线MN的距离d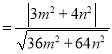
，
将
1，代入得d
，
因为0＜n2≤3，所以dmin
，又
1，
故原点O到直线MN的距离的最小值为
.
练习册系列答案
阅读快车系列答案
相关题目
