题目内容
设双曲线
-
=1(a>0,b>0)的左、右焦点分别为F1、F2,离心率为e,过F2的直线与双曲线的右支交于A、B两点,若△F1AB是以A为直角顶点的等腰直角三角形,则e2=______.
| x2 |
| a2 |
| y2 |
| b2 |
设|AF1|=|AB|=m,
则|BF1|=
m,|AF2|=m-2a,|BF2|=
m-2a,
∵|AB|=|AF2|+|BF2|=m,
∴m-2a+
m-2a=m,
∴4a=
m,
∴|AF2|=(1-
)m,
∵△AF1F2为Rt三角形,
∴|F1F2|2=|AF1|2+|AF2|2
∴4c2=(
-
)m2,
∵4a=
m,
∴4c2=(
-
)×8a2,
∴e2=5-2
.
故答案为:5-2
.
则|BF1|=
| 2 |
| 2 |
∵|AB|=|AF2|+|BF2|=m,
∴m-2a+
| 2 |
∴4a=
| 2 |
∴|AF2|=(1-
| ||
| 2 |
∵△AF1F2为Rt三角形,
∴|F1F2|2=|AF1|2+|AF2|2
∴4c2=(
| 5 |
| 2 |
| 2 |
∵4a=
| 2 |
∴4c2=(
| 5 |
| 2 |
| 2 |
∴e2=5-2
| 2 |
故答案为:5-2
| 2 |

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
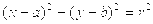 的圆心为抛物线
的圆心为抛物线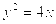 的焦点,直线3x+4y+2=0与圆C相切,则该圆的方程为( ).
的焦点,直线3x+4y+2=0与圆C相切,则该圆的方程为( ).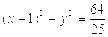
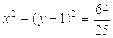
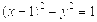
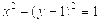
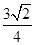 ,则点A的坐标为( )
,则点A的坐标为( )