题目内容
14.不等式组$\left\{\begin{array}{l}{|x-1|-3<0}\\{a-2x>0}\end{array}\right.$的解集为{x|-2<x<3},则实数a的取值范围是( )| A. | a=4 | B. | a=6 | C. | a≤6 | D. | a≥6 |
分析 由|x-1|-3<0,得-2<x<4,由a-2x>0,得x<$\frac{a}{2}$,再由不等式组$\left\{\begin{array}{l}{|x-1|-3<0}\\{a-2x>0}\end{array}\right.$的解集为{x|-2<x<3},能求出a的值.
解答 解:∵不等式组$\left\{\begin{array}{l}{|x-1|-3<0}\\{a-2x>0}\end{array}\right.$的解集为{x|-2<x<3},
由|x-1|-3<0,得-2<x<4,
由a-2x>0,得x<$\frac{a}{2}$,
∴$\frac{a}{2}=3$,解得a=6.
故选:B.
点评 本题考查不等式的解法,是基础题,解题时要认真审题,注意含绝对值不等式的性质的合理运用.

练习册系列答案
相关题目
3.等差数列{an}中,a5=4,a9=10,则a13=( )
| A. | 25 | B. | 16 | C. | 14 | D. | 12 |
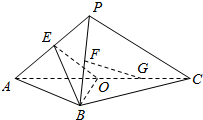 如图,E、F、O分别是PA,PB,AC的中点,G是OC的中点,求证:FG∥平面BOE(两种方法证明).
如图,E、F、O分别是PA,PB,AC的中点,G是OC的中点,求证:FG∥平面BOE(两种方法证明).