题目内容
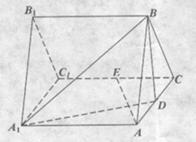
(本小题满分13分)如图,三棱柱ABC—A1B1C1的所有棱长都是2,又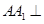 平面
平面
ABC,D、E分别是AC、CC1的中点。
(1)求证: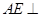 平面A1BD;
平面A1BD;
(2)求二面角D—BA1—A的余弦值;
(3)求点B1到平面A1BD的距离。
 平面
平面ABC,D、E分别是AC、CC1的中点。
(1)求证:
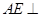 平面A1BD;
平面A1BD;(2)求二面角D—BA1—A的余弦值;
(3)求点B1到平面A1BD的距离。

(Ⅰ)证明:以DA所在直线为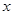 轴,过D作AC 的垂线为
轴,过D作AC 的垂线为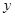 轴,DB所在直线为
轴,DB所在直线为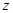 轴建立空间直角坐标系
轴建立空间直角坐标系
则A(1,0,0),C(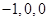 ),E(
),E(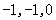 ),A1(
),A1(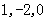 ),C1(
),C1(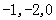 ),B(
),B(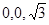 )
)
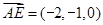 ,
,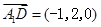 ,
,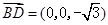
∵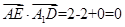 ∴
∴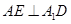 ………………………………………………2分
………………………………………………2分
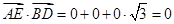 ∴
∴ 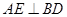 …………………………………………4分
…………………………………………4分
又A1D与BD相交
∴AE⊥面A1BD ……………………………………………………………5分
(其它证法可平行给分)
(Ⅱ)设面DA1B的法向量为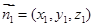
由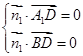 ,
,
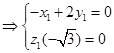 ,取
,取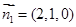 ……………………………7分
……………………………7分
设面AA1B的法向量为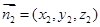 ,
,
则由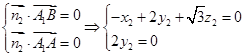 ,取
,取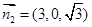 ………………9分
………………9分
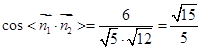
故二面角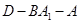 的余弦值为
的余弦值为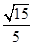 …………………………………10分
…………………………………10分
(Ⅲ)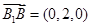 ,平面A1BD的法向量取
,平面A1BD的法向量取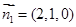
则B1到平面A1BD的距离为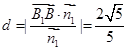 …………………………13分
…………………………13分
 轴,过D作AC 的垂线为
轴,过D作AC 的垂线为 轴,DB所在直线为
轴,DB所在直线为 轴建立空间直角坐标系
轴建立空间直角坐标系则A(1,0,0),C(
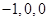 ),E(
),E(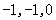 ),A1(
),A1(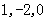 ),C1(
),C1(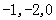 ),B(
),B(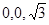 )
)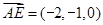 ,
,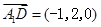 ,
,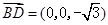
∵
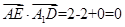 ∴
∴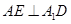 ………………………………………………2分
………………………………………………2分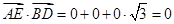 ∴
∴ 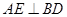 …………………………………………4分
…………………………………………4分又A1D与BD相交
∴AE⊥面A1BD ……………………………………………………………5分
(其它证法可平行给分)
(Ⅱ)设面DA1B的法向量为
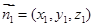
由
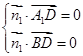 ,
,
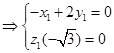 ,取
,取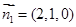 ……………………………7分
……………………………7分设面AA1B的法向量为
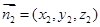 ,
,则由
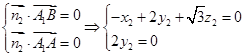 ,取
,取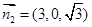 ………………9分
………………9分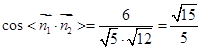
故二面角
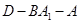 的余弦值为
的余弦值为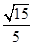 …………………………………10分
…………………………………10分(Ⅲ)
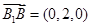 ,平面A1BD的法向量取
,平面A1BD的法向量取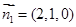
则B1到平面A1BD的距离为
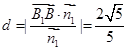 …………………………13分
…………………………13分略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
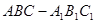 中,
中,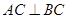 ,
,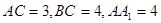 ,点
,点 是
是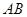 的中点,
的中点,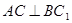 ;
;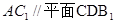 ;
; 与平面
与平面 所成角的正切值.
所成角的正切值.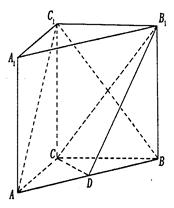
 、
、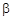 是两个不同的平面,则下列命题正确的是( )
是两个不同的平面,则下列命题正确的是( )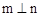 、 m
、 m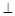
 ∥n
∥n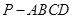 的底面是边长为1的正方形,
的底面是边长为1的正方形,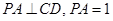 ,
,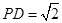 ,
, 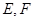 为
为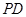 上两点,且
上两点,且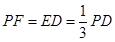 .
.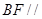 面
面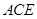 ;
;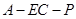 的正切值.
的正切值.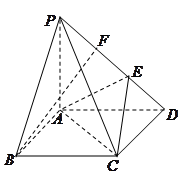
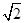 ,E为PD上一点,PE = 2ED.
,E为PD上一点,PE = 2ED.
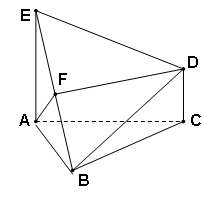
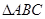 中,
中,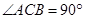 ,AB=8,
,AB=8,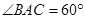 ,PC
,PC 面ABC,PC=4,M是AB边上的一动
面ABC,PC=4,M是AB边上的一动



 中,点
中,点 为线段
为线段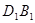 上的动点,点
上的动点,点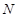 为线段
为线段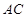 上的动点,则与线段
上的动点,则与线段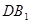 相交且互相平分的线段
相交且互相平分的线段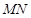 有( )
有( )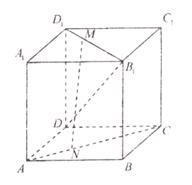

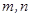 是不同的直线,
是不同的直线,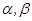 是不重合的平面,给出下面三个命题:
是不重合的平面,给出下面三个命题: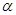 //
//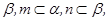 则
则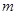 //
//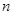 .
.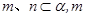 //
//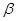 ,
,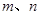 是两条异面直线,若
是两条异面直线,若