题目内容
【题目】某医药研究所开发一种新药,在试验药效时发现:如果成人按规定剂量服用,那么服药后每毫升血液中的含药量y(微克)与时间x(小时)之间满足y= 其对应曲线(如图所示)过点
其对应曲线(如图所示)过点![]() .
.

(1)试求药量峰值(y的最大值)与达峰时间(y取最大值时对应的x值);
(2)如果每毫升血液中含药量不少于1微克时治疗疾病有效,那么成人按规定剂量服用该药后一次能维持多长的有效时间(精确到0.01小时)?
【答案】(1)y取最大值时,对应的x值为1.(2)3.85小时
【解析】(1)由曲线过点![]() ,可得
,可得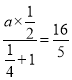 ,故a=8.
,故a=8.
当0<x<1时,y=![]() =4,
=4,
当x≥1时,设2x-1=t,可知t≥1,
y=![]() ≤
≤![]() =4(当且仅当t=1,即x=1时,等号成立).
=4(当且仅当t=1,即x=1时,等号成立).
综上可知ymax=4,且当y取最大值时,对应的x值为1.
所以药量峰值为4微克,达峰时间为1小时.
(2)当0<x<1时,由![]() =1,可得x2-8x+1=0,
=1,可得x2-8x+1=0,
解得x=4±![]() ,又4+
,又4+![]() >1,故x=4-
>1,故x=4-![]() .
.
当x≥1时,设2x-1=t,则t≥1,![]() =1,可得
=1,可得![]() =1,解得t=4±
=1,解得t=4±![]() ,
,
又t≥1,故t=4+![]() ,所以2x-1=4+
,所以2x-1=4+![]() ,可得x=log2(4+
,可得x=log2(4+![]() )+1.
)+1.
由图像知当y≥1时,对应的x的取值范围是[4-![]() ,log2(4+
,log2(4+![]() )+1],
)+1],
log2(4+![]() )+1-(4-
)+1-(4-![]() )≈3.85,
)≈3.85,
所以成人按规定剂量服用该药后一次能维持大约3.85小时的有效时间.

【题目】某种产品的广告费支出![]() 与销售额
与销售额![]() (单位:万元)之间有如下对应数据:
(单位:万元)之间有如下对应数据:
|
|
|
|
|
|
|
|
|
|
|
|
(1)求回归直线方程;
(2)试预测广告费支出为![]() 万元时,销售额多大?
万元时,销售额多大?
(3)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的绝对值不超过![]() 的概率.(参考数据:
的概率.(参考数据: 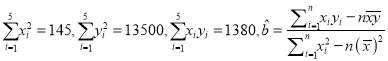 .
.
【题目】一鲜花店一个月(30天)某种鲜花的日销售量与销售天数统计如下:
日销售量(枝) | 0~49 | 50~99 | 100~149 | 150~199 | 200~250 |
销售天数(天) | 3天 | 3天 | 15天 | 6天 | 3天 |
将日销售量落入各组区间的频率视为概率.
(1)试求这30天中日销售量低于100枝的概率;
(2)若此花店在日销售量低于100枝的6天中选择2天作促销活动,求这2天的日销售量都低于50枝的概率(不需要枚举基本事件).