Question

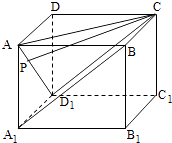
【题目】如图，在四棱锥P﹣ABCD中，AD∥BC，∠ADC=∠PAB=90°，BC=CD= AD．E为棱AD的中点，异面直线PA与CD所成的角为90°．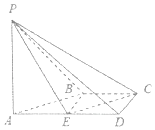
（1）在平面PAB内找一点M，使得直线CM∥平面PBE，并说明理由；
（2）若二面角P﹣CD﹣A的大小为45°，求二面角P﹣CE﹣B的余弦值．

Answer 1

【答案】
（1）解：延长AB交直线CD于点M，

∵点E为AD的中点，∴ ，

∵ ，∴ED=BC，

∵AD∥BC，即ED∥BC．∴四边形BCDE为平行四边形，即EB∥CD．

∵AB∩CD=M，∴M∈CD，∴CM∥BE，

∵BE平面PBE，CMPBE∴CM∥平面PBE，

∵M∈AB，AB平面PAB，∴M∈平面PAB，故在平面PAB内可以找到一点M（M=AB∩CD），使得直线CM∥平面PBE

（2）解：∵∠ADC=∠PAB=90°，异面直线PA与CD所成的角为90°，即AP⊥CD又AB∩CD=M，

∴AP⊥平面ABCD．

又∠ADC=90°即CD⊥AD

∴CD⊥平面PAD

∴CD⊥PD．

因此∠PDA是二面角P﹣CD﹣A的平面角，其大小为45°．

∴PA=AD．

建立如图所示的空间直角坐标系，不妨设AD=2，则 ．

∴P（0，0，2），E（0，1，0），C（﹣1，2，0），B（﹣1，1，0）

∴ ， =（0，1，﹣2）， ，

易知平面BCE的法向量为

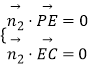设平面PCE的法向量为 ，则 ，可得： ．

令y=2，则x=2，z=1，∴ ．

设二面角P﹣CE﹣B的平面角为θ，

则 = = ．

∴二面角P﹣CE﹣B的余弦值为 ．

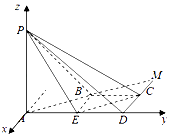
【解析】（1）延长AB交直线CD于点M，证明CM∥BE，即可使得直线CM∥平面PBE；（2）建立如图所示的空间直角坐标系，不妨设AD=2，则 ．求出平面的法向量，即可求二面角P﹣CE﹣B的余弦值．
【考点精析】根据题目的已知条件，利用直线与平面平行的判定的相关知识可以得到问题的答案，需要掌握平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行．