题目内容
【题目】已知四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,E是BC中点,M是PD上的中点,F是PC上的动点. (Ⅰ)求证:平面AEF⊥平面PAD
(Ⅱ)直线EM与平面PAD所成角的正切值为 ![]() ,当F是PC中点时,求二面角C﹣AF﹣E的余弦值.
,当F是PC中点时,求二面角C﹣AF﹣E的余弦值.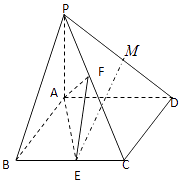
【答案】证明:(Ⅰ)连接AC, 
∵底面ABCD为菱形,∠ABC=60°,
∴△ABC是正三角形,
∵E是BC中点,∴AE⊥BC,
又AD∥BC,∴AE⊥AD,
∵PA⊥平面ABCD,AE平面ABCD,∴PA⊥AE,
又PA∩AE=A,
∴AE⊥平面PAD,
又AE平面AEF,
∴平面AEF⊥平面PCD.
(Ⅱ)解:由(Ⅰ)得,AE,AD,AP两两垂直,
以AE,AD,AP所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系, 
∵AE⊥平面PAD,∴∠AME就是EM与平面PAD所成的角,
在Rt△AME中,tan ![]() ,即
,即 ![]() =
= ![]() ,
,
设AB=2a,则AE= ![]() ,得AM=
,得AM= ![]() ,
,
又AD=AB=2a,设PA=2b,则M(0,a,b),
∴AM= ![]() =
= ![]() ,
,
从而b=a,∴PA=AD=2a,
则A(0,0,0),B( ![]() ,﹣a,0),C(
,﹣a,0),C( ![]() ),D(0,2a,0),P(0,0,2a),E(
),D(0,2a,0),P(0,0,2a),E( ![]() ),F(
),F( ![]() ,
, ![]() ,a),
,a),
∴ ![]() =(
=( ![]() ),
), ![]() =(
=( ![]() ,
, ![]() ,a),
,a), ![]() =(﹣
=(﹣ ![]() ),
),
设 ![]() =(x,y,z)是平面AEF的一个法向量,
=(x,y,z)是平面AEF的一个法向量,
则  ,取z=a,得
,取z=a,得 ![]() =(0,﹣2a,a),
=(0,﹣2a,a),
又BD⊥平面ACF,∴ ![]() =(﹣
=(﹣ ![]() )是平面ACF的一个法向量,
)是平面ACF的一个法向量,
设二面角C﹣AF﹣E的平面角为θ.
则cosθ=  =
= ![]() =
= ![]() .
.
∴二面角C﹣AF﹣E的余弦值为 ![]() .
.
【解析】(Ⅰ)连接AC,推导出AE⊥BC,AE⊥AD,PA⊥AE,由此能证明平面AEF⊥平面PCD. (Ⅱ)以AE,AD,AP所在直线分别为x轴,y轴,z轴建立空间直角坐标系,利用向量法能求出二面角C﹣AF﹣E的余弦值.
【考点精析】通过灵活运用平面与平面垂直的判定和空间角的异面直线所成的角,掌握一个平面过另一个平面的垂线,则这两个平面垂直;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 即可以解答此题.
即可以解答此题.


