题目内容
线段PQ是椭圆
+
=1过M(1,0)的一动弦,且直线PQ与直线x=4交于点S,则
+
=______.
| x2 |
| 4 |
| y2 |
| 3 |
| |SM| |
| |SP| |
| |SM| |
| |SQ| |
设直线PQ的方程为y=k(x-1),所以S(4,3k),
设P,Q的横坐标分别为x1,x2,
联立
解得(3+4k2)x2-8k2x+4k2-12=0,
所以x1+x2=
x1•x2=
,
+
=
+
=3×
=3×
=3×
=3×
=2.
故答案为:2.
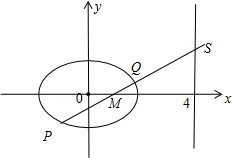
设P,Q的横坐标分别为x1,x2,
联立
|
所以x1+x2=
| 8k2 |
| 3+4k2 |
x1•x2=
| 4k2-12 |
| 3+4k2 |
| |SM| |
| |SP| |
| |SM| |
| |SQ| |
| 3 |
| 4-x1 |
| 3 |
| 4-x2 |
=3×
| 8-(x1+x2) |
| (4-x1)(4-x2) |
=3×
| 8-(x1+x2) |
| 16-4(x1+x2)+x1x2 |
=3×
8-
| ||||
16-4×
|
=3×
| 24k2+24 |
| 36+36k2 |
=2.
故答案为:2.


练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目