题目内容

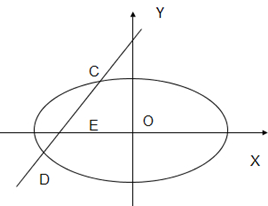
如图，已知椭圆
x2
a2
+
y2
b2
（a＞b＞0）的离心率e=
6
3
，短轴长为2．
（1）求椭圆的方程．
（2）已知定点E（-1，0），若直线y=kx+2（k≠0）与椭圆交于C、D两点．问：是否存在k的值，使以CD为直径的圆过E点？请说明理由．
（1）∵椭圆
x2
a2
+
y2
b2
（a＞b＞0）的离心率e=
6
3
，短轴长为2，
∴
a2-b2
a
=
6
3
b=1
，
∴a=
3
，b=1，
椭圆方程为
x2
3
+y2=1．
（2）假若存在这样的k值，由
y=kx+2
x2+3y2-3=0
得（1+3k2）x2+12kx+9=0．
∴△=（12k）2-36（1+3k2）＞0①
设C（x1，y1）、D（x2，y2），则
x1+x2=-
12k
1+3k2
x1•x2=
9
1+3k2
②
若以CD为直径的圆过E点，则
EC
•
ED
=0，即（x1+1）（x2+1）+y1y2=0，
而y1y2=（kx1+2）（kx2+2）=k2x1x2+2k（x1+x2）+4，
代入上式得，化为（k2+1）x1x2+（2k+1）（x1+x2）+5=0．
把（**）代入上式得
9k2
1+3k2
-
12k(2k+1)
1+3k2
+5=0
解得k=
7
6
，满足k2＞1．
∴存在k=
7
6
，使得以线段CD为直径的圆过E点．
练习册系列答案
相关题目
如图，已知抛物线C：y2=4x焦点为F，直线l经过点F且与抛物线C相交于A，B两点
（Ⅰ）若线段AB的中点在直线y=1上，求直线l的方程；
（Ⅱ）若线段|AB|=20，求直线l的方程．
已知平面内一动点P到点F（2，0）的距离比点P到y轴的距离大2，
（Ⅰ）求动点P的轨迹C的方程；
（Ⅱ）过点F且斜率为2
2
的直线交轨迹C于A（x1，y1），B（x2，y2）（x1＜x2）两点，P（x3，y3）（x3≥0）为轨迹C上一点，若
OP
=
OA
+λ
OB
，求λ的值．
已知圆C：x2+y2-2x+4y-4=0，
（Ⅰ）若过定点（-2，0）的直线l与圆C相切，求直线l的方程；
（Ⅱ）若过定点（-1，0）且倾斜角为
π
6
的直线l与圆C相交于A，B两点，求线段AB的中点P的坐标．
已知椭圆C1的方程为
x2
4
+y2=1，双曲线C2的左、右焦点分别为C1的左、右顶点，而C2的左、右顶点分别是C1的左、右焦点．
（Ⅰ）求双曲线C2的方程；
（Ⅱ）若直线l：y=kx+
2
与椭圆C1及双曲线C2都恒有两个不同的交点，且l与C2的两个交点A和B满足
OA
•
OB
＜6（其中O为原点），求k的取值范围．
已知直线l：y=2x与抛物线C：y=
1
4
x2交于A（xA，yA）、O（0，0）两点，过点O与直线l垂直的直线交抛物线C于点B（xB，yB）．如图所示．
（1）求抛物线C的焦点坐标；
（2）求经过A、B两点的直线与y轴交点M的坐标；
（3）过抛物线y=
1
4
x2的顶点任意作两条互相垂直的直线，过这两条直线与抛物线的交点A、B的直线AB是否恒过定点，如果是，指出此定点，并证明你的结论；如果不是，请说明理由．
线段PQ是椭圆
x2
4
+
y2
3
=1过M（1，0）的一动弦，且直线PQ与直线x=4交于点S，则
|SM|
|SP|
+
|SM|
|SQ|
=______．
直线与双曲线x2-4y2=4交于A、B两点，若线段AB的中点坐标为（8，1），则直线的方程为______．
如图，圆O的半径为定长r，A是圆O外一定点，P是圆上任意一点．线段AP的垂直平分线l和直线OP相交于点Q，当点P在圆上运动时，点Q的轨迹是（　　）
A．椭圆B．圆C．双曲线D．直线

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网