题目内容
(本小题满分12分)在数列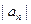 ,
,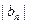 是各项均为正数的等比数列,设
是各项均为正数的等比数列,设 .(Ⅰ)数列
.(Ⅰ)数列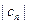 是否为等比数列?证明你的结论;(Ⅱ)设数列
是否为等比数列?证明你的结论;(Ⅱ)设数列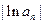 ,
,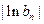 的前
的前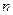 项和分别为
项和分别为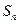 ,
,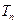 .若
.若 ,
,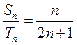 ,求数列
,求数列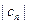 的前
的前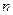 项和.
项和.
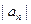 ,
,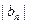 是各项均为正数的等比数列,设
是各项均为正数的等比数列,设 .(Ⅰ)数列
.(Ⅰ)数列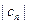 是否为等比数列?证明你的结论;(Ⅱ)设数列
是否为等比数列?证明你的结论;(Ⅱ)设数列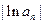 ,
,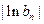 的前
的前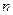 项和分别为
项和分别为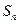 ,
,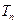 .若
.若 ,
,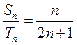 ,求数列
,求数列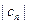 的前
的前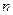 项和.
项和.(Ⅰ) 为等比数列(Ⅱ)数列
为等比数列(Ⅱ)数列 的前
的前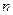 项和为
项和为
 为等比数列(Ⅱ)数列
为等比数列(Ⅱ)数列 的前
的前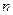 项和为
项和为
解:(Ⅰ) 是等比数列. 2分
是等比数列. 2分
证明:设 的公比为
的公比为 ,
,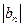 的公比为
的公比为 ,则
,则
 ,故
,故 为等比数列. 5分
为等比数列. 5分
(Ⅱ)数列 和
和 分别是公差为
分别是公差为 和
和 的等差数列.
的等差数列.
由条件得 ,即
,即
 . 7分
. 7分
故对 ,
, ,…,
,…,
 .
.
于是

将 代入得
代入得 ,
, ,
, . 10分
. 10分
从而有 .
.
所以数列 的前
的前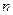 项和为
项和为
 . 12分
. 12分
 是等比数列. 2分
是等比数列. 2分证明:设
 的公比为
的公比为 ,
,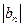 的公比为
的公比为 ,则
,则 ,故
,故 为等比数列. 5分
为等比数列. 5分(Ⅱ)数列
 和
和 分别是公差为
分别是公差为 和
和 的等差数列.
的等差数列.由条件得
 ,即
,即 . 7分
. 7分故对
 ,
, ,…,
,…, .
.于是

将
 代入得
代入得 ,
, ,
, . 10分
. 10分从而有
 .
.所以数列
 的前
的前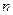 项和为
项和为 . 12分
. 12分
练习册系列答案
相关题目
 的前n项和为
的前n项和为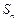 ,已知
,已知 .
.
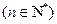 ,求数列
,求数列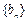 的前n项和
的前n项和 .
.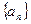 中,若
中,若 ,则称数列
,则称数列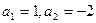 ,试写出该数列的前6项,并求出该6项之和;
,试写出该数列的前6项,并求出该6项之和;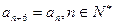 ;
;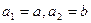 ,若数列
,若数列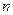 项和
项和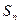 。
。 中,已知
中,已知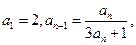 依次计算
依次计算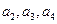 可猜得
可猜得 的表达式为()
的表达式为()




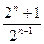 B
B C.
C.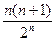 D.1-
D.1-
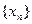 满足
满足 若
若 则数列
则数列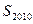 为 ( )
为 ( )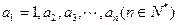 的法则如下:如果
的法则如下:如果 为自然数,则写
为自然数,则写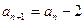 ,否则就写
,否则就写 ,则
,则 =_____。(注意:0是自然数)
=_____。(注意:0是自然数)