题目内容
12．若y=15sin[$\frac{π}{6}$（x+1）]表示一个振动，则这个振动的初相是$\frac{π}{6}$．分析 化简函数的解析式，即可求出初相．
解答 解：y=15sin[$\frac{π}{6}$（x+1）]=15sin（$\frac{π}{6}x$+$\frac{π}{6}$），这个振动的初相是$\frac{π}{6}$．
故答案为：$\frac{π}{6}$．
点评 本题考查三角函数的解析式的应用，此时的物理意义，是基础题．
练习册系列答案
相关题目
2．
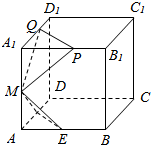如图：已知棱长为l的正方体ABCD-A1B1C1D1中，E，F，M分别是AB、AD、AA1的中点，又P、Q分别在线段A1B1、A1D1上，且A1P=A1Q=x，0＜x＜1，设平面MEF∩平面MPQ=l，则下列结论中不成立的是（ ）
如图：已知棱长为l的正方体ABCD-A1B1C1D1中，E，F，M分别是AB、AD、AA1的中点，又P、Q分别在线段A1B1、A1D1上，且A1P=A1Q=x，0＜x＜1，设平面MEF∩平面MPQ=l，则下列结论中不成立的是（ ）| A． | l∥平面ABCD | B． | 平面MEF与平面MPQ不垂直 | ||
| C． | l⊥BC1 | D． | 当x变化时，l是定直线 |
20．已知中心在坐标原点的椭圆和双曲线的焦点相同，左、右焦点分别为F1，F2，这两条曲线在第一象限的交点为P，且△PF1F2是以PF1为斜边的等腰直角三角形，则椭圆和双曲线的离心率之积为（ ）
| A． | 1 | B． | 2$\sqrt{2}$+3 | C． | 2$\sqrt{2}$ | D． | 3一2$\sqrt{2}$ |
1．下列大小关系正确的是（ ）
| A． | $log_4^{0.3}＜{0.4^3}＜{3^{0.4}}$ | B． | ${0.4^3}＜log_4^{0.3}＜{3^{0.4}}$ | ||
| C． | $log_4^{0.3}＜{3^{0.4}}＜{0.4^3}$ | D． | ${0.4^3}＜{3^{0.4}}＜log_4^{0.3}$ |