题目内容
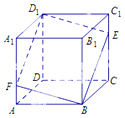
【题目】已知长方体AC1中，AD=AB=2，AA1=1，E为D1C1的中点，如图所示． 
（Ⅰ）在所给图中画出平面ABD1与平面B1EC的交线（不必说明理由）；
（Ⅱ）证明：BD1∥平面B1EC；
（Ⅲ）求平面ABD1与平面B1EC所成锐二面角的大小．
【答案】解：（Ⅰ）连接BC1交B1C于M，则直线ME即为平面ABD1与平面B1EC的
交线，如图所示；
（Ⅱ）由（Ⅰ）因为在长方体AC1中，所以M为BC1的中点，又E为D1C1的中点
所以在△D1C1B中EM是中位线，所以EM∥BD1 ，
又EM平面B1EC，BD1平面B1EC，
所以BD1∥平面B1EC；
（Ⅲ）因为在长方体AC1中，所以AD1∥BC1 ，
平面ABD1即是平面ABC1D1 ， 过平面B1EC上
点B1作BC1的垂线于F，如平面图①，
因为在长方体AC1中，AB⊥平面B1BCC1 ， B1F平面B1BCC1 ， 所以B1F⊥AB，BC1∩AB=B，
所以B1F⊥平面ABD1于F．
过点F作直线EM的垂线于N，如平面图②，
连接B1N，由三垂线定理可知，B1N⊥EM．由二面角的平面角定义可知，在Rt△B1FN中，∠B1NF即是平面ABD1与平面B1EC所成锐二面角的平面角．
因长方体AC1中，AD=AB=2，AA1=1，在平面图①中， 
，
， 
，C1E=1，在平面图②中，由△EMC1相似△FMN1可知 
= 
= 
，
所以tan∠B1NF= 
= 
，
所以平面ABD1与平面B1EC所成锐二面角的大小为arctan2．
空间向量解法：
（Ⅰ）见上述．
（Ⅱ）因为在长方体AC1中，所以DA，DC，DD1两两垂直，于是以DA，DC，DD1所在直线分别为x，y，z轴，以D为坐标原点，建立空间直角坐标系，如图所示，
因为AD=AB=2，AA1=1，所以D（0，0，0），D1（0，0，1），B（2，2，0），B1（2，2，1），C（0，2，0），E（0，1，1）．所以 
， 
， 
，
令平面B1EC的一个法向量为 
所以 
， 
，从而有，
，即 
，不妨令x=﹣1，
得到平面B1EC的一个法向量为 
，
而 
，所以 
，又因为BD1平面B1EC，
所以BD1∥平面B1EC．
（Ⅲ）由（Ⅱ）知 
， ，令平面ABD1的一个法向量为 
，
所以 
， 
，从而有， 
，即 
，不妨令x=1，
得到平面ABD1的一个法向量为 
，
因为 
= 
．
所以平面ABD1与平面B1EC所成锐二面角的大小为 
【解析】（Ⅰ）连接BC1交B1C于M即可得到平面ABD1与平面B1EC的交线；（Ⅱ）根据线面平行的判定定理即可证明：BD1∥平面B1EC；（Ⅲ）方法1，根据几何法作出二面角的平面角即可求平面ABD1与平面B1EC所成锐二面角的大小．方法2，建立坐标系，求出平面的法向量，利用向量法进行求解．
