题目内容
2012年10月莫言获得诺贝尔文学奖后,其家乡山东高密政府准备投资6.7亿元打造旅游带,包括莫言旧居周围的莫言文化体验区,红高粱文化休闲区,爱国主义教育基地等;为此某文化旅游公司向社会公开征集旅游带建设方案,在收到的方案中甲、乙、丙三个方案引起了专家评委的注意,现已知甲、乙、丙三个方案能被选中的概率分别为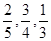 ,且假设各自能否被选中是无关的.
,且假设各自能否被选中是无关的.
(1)求甲、乙、丙三个方案只有两个被选中的概率;
(2)记甲、乙、丙三个方案被选中的个数为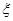 ,试求
,试求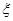 的期望.
的期望.
(1)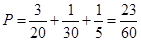
(2)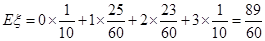
解析试题分析:解:记甲、乙、丙三个方案被选中的事件分别为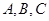 ,则
,则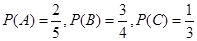 .
.
(1)“只有两个方案被选中”可分为三种情形:
①甲未被选中,乙、丙被选中,概率为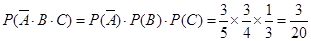 .……1分
.……1分
②乙未被选中,甲、丙被选中,概率为 .……2分
.……2分
③丙未被选中,甲、乙被选中,概率为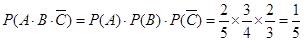 .……3分
.……3分
以上三种情况是互斥的. 因此只有两个方案被选中的概率为: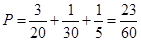 .……5分
.……5分
(2)由题意可知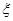 的可能取值为0,1,2,3.……6分
的可能取值为0,1,2,3.……6分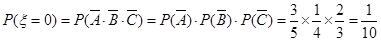 ;
; 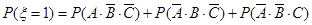
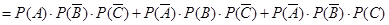
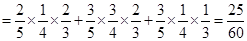 ;
;
由(1)知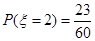 ;
;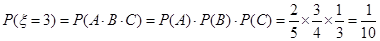 .……10分
.……10分
故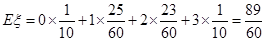 .……12分
.……12分
考点:独立事件的概率的乘法公式
点评:主要是考查概率的求解,以及分布列以及数学期望的运用,属于中档题。

某人在如图所示的直角边长为4米的三角形地块的每个格点(指纵、横直线的交叉点以及三角形的顶点)处都种了一株相同品种的作物。根据历年的种植经验,一株该种作物的年收货量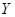 (单位:kg)与它的“相近”作物株数
(单位:kg)与它的“相近”作物株数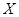 之间的关系如下表所示:
之间的关系如下表所示: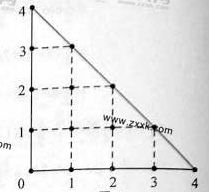
| X | 1 | 2 | 3 | 4 |
| Y | 51 | 48 | 45 | 42 |
这里,两株作物“相近”是指它们之间的直线距离不超过1米。
(Ⅰ)完成下表,并求所种作物的平均年收获量;
| Y | 51 | 48 | 45 | 42 |
| 频数 | | 4 | | |
某市直小学为了加强管理,对全校教职工实行新的临时事假制度:“每位教职工每月在正常的工作时间,临时有事,可请假至多三次,每次至多一小时”.现对该制度实施以来50名教职工请假的次数进行调查统计,结果如下表所示:
| 请假次数 |  |  |  |  |
| 人数 | 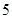 | 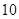 | 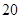 | 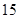 |
(1)从该小学任选两名教职工,用
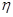 表示这两人请假次数之和,记“函数
表示这两人请假次数之和,记“函数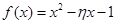 在区间
在区间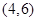 上有且只有一个零点”为事件
上有且只有一个零点”为事件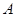 ,求事件
,求事件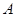 发生的概率
发生的概率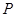 ;
;(2)从该小学任选两名职工,用
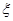 表示这两人请假次数之差的绝对值,求随机变量
表示这两人请假次数之差的绝对值,求随机变量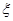 的分布列及数学期望
的分布列及数学期望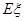 .
. 山东省某示范性高中为了推进新课程改革,满足不同层次学生的需求,决定从高一年级开始,在每周的周一、周三、周五的课外活动期间同时开设数学、物理、化学、生物和信息技术辅导讲座,每位有兴趣的同学可以在期间的任何一天参加任何一门科目的辅导讲座,也可以放弃任何一门科目的辅导讲座.(规定:各科达到预先设定的人数时称为满座,否则称为不满座)统计数据表明,各学科讲座各天的满座概率如下表:
| | 信息技术 | 生物 | 化学 | 物理 | 数学 |
| 周一 | 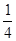 | 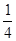 | 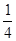 | 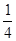 |  |
| 周三 |  |  |  |  | 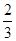 |
| 周五 |  |  |  |  | 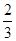 |
(Ⅱ)设周三各辅导讲座满座的科目数为
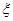 ,求随即变量
,求随即变量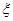 的分布列和数学期望.
的分布列和数学期望. 我区高三期末统一测试中某校的数学成绩分组统计如下表:
| 分组 | 频数 | 频率 |
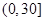 | 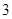 | 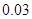 |
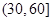 | 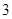 | 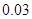 |
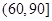 | 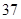 | 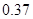 |
 | 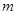 | 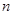 |
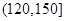 | 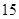 | 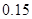 |
| 合计 | 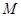 | 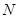 |
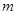 、
、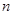 、
、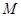 、
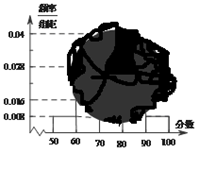
、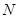 的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图;
的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图;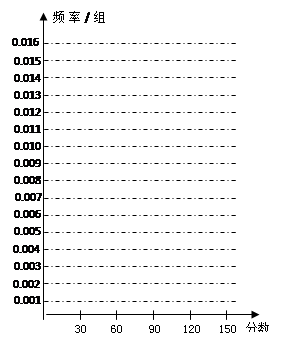
(2)若我区参加本次考试的学生有600人,试估计这次测试中我区成绩在
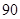 分以上的人数;
分以上的人数;(3)若该校教师拟从分数不超过60的学生中选取2人进行个案分析,求被选中2人分数不超过30分
的概率.
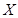 位,若连续抽取到两位愿意购买本地家禽的市民,或
位,若连续抽取到两位愿意购买本地家禽的市民,或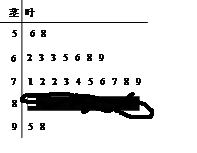
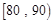 之间的频数,并计算频率分布直方图中
之间的频数,并计算频率分布直方图中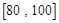 之间的学生中任选两人进行某项研究,求至少有一人分数在
之间的学生中任选两人进行某项研究,求至少有一人分数在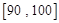 之间的概率.
之间的概率.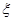 的分布列;
的分布列; 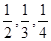 ,且每位同学能否通过考试时相互独立的。
,且每位同学能否通过考试时相互独立的。 ,求这三位同学中恰好有一位同学考上大学的概率。
,求这三位同学中恰好有一位同学考上大学的概率。