题目内容
一袋中有6个黑球，4个白球．
(1)依次取出3个球，不放回，已知第一次取出的是白球，求第三次取到黑球的概率；
(2)有放回地依次取出3球，已知第一次取的是白球，求第三次取到黑球的概率；
(3)有放回地依次取出3球，求取到白球个数X的分布列、期望和方差．
（1）
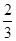（2）
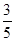（3）
解析试题分析：(1)法一：设A＝“第一次取到白球”，B＝“第二次取到白球”，C＝“第三次取到白球”，则在A发生的条件下，袋中只剩6个黑球和3个白球，
则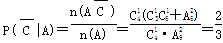
. 4分
法二：同上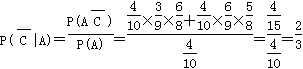
. 4分
(2)∵每次取之前袋中球的情况不变，
∴n次取球的结果互不影响．∴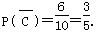
6分
(3)设“摸一次球，摸到白球”为事件D，则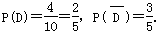
∵这三次摸球互不影响，显然这个试验为独立重复试验，X服从二项分布，即X～B(3，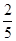
)．
∴
，
，
，
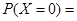
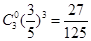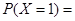
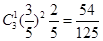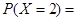
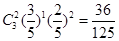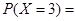
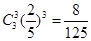10分
∴X的分布列为：
显然这个试验为独立重复试验，X服从二项分布，即X～B(3，X 0 1 2 3 P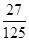 
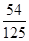
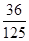
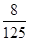
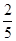)． 12分
所以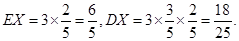
14分
考点：本小题主要考查条件概率，对立重复试验，二项分布，期望等.
点评：此类问题运算比较麻烦，难度一般不大，考查学生分析问题、转化问题、解决问题的能力和运算能力.
练习册系列答案
相关题目
我区高三期末统一测试中某校的数学成绩分组统计如下表：
| 分组 | 频数 | 频率 |
 |  |  |
 | | |
 |  |  |
 |  |  |
 |  |  |
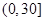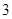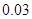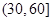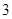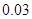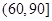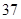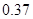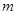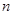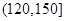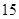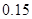| 合计 |  |  |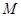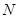
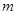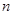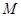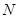、、、的值，并根据表中所给数据在下面给出的坐标系中画出频率分布直方图；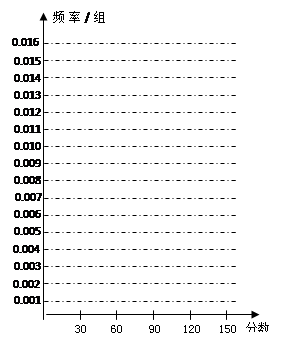
（2）若我区参加本次考试的学生有600人，试估计这次测试中我区成绩在
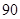分以上的人数；（3）若该校教师拟从分数不超过60的学生中选取2人进行个案分析，求被选中2人分数不超过30分
的概率．
（
）
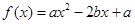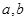
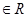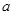从集合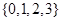
中任取一个元素，
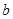从集合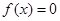
恰有两个不相等实根的概率；
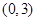中任取一个数，
中任取一个数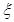
表示该同学猜灯谜结束后所得奖品的总金额。
;
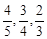,且每个问题回答正确与否相互独立.
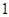次，求在这一枪出现空弹的概率；
次，求在这三枪中出现空弹的概率； 
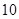的等边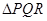
，甲射手用实弹瞄准了三角形
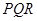区域随机射击，且弹孔都落在三角形