题目内容
已知点P(4,4),圆C: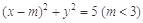 与椭圆E:
与椭圆E: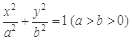 有一个公共点A(3,1),F1、F2分别是椭圆的左、右焦点,直线PF1与圆C相切.
有一个公共点A(3,1),F1、F2分别是椭圆的左、右焦点,直线PF1与圆C相切.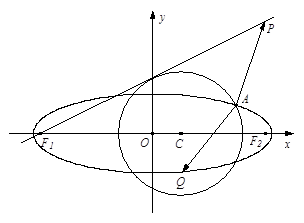
(1)求m的值与椭圆E的方程;
(2)设Q为椭圆E上的一个动点,求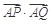 的取值范围.
的取值范围.
(Ⅰ)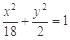 .(Ⅱ) [-12,0].
.(Ⅱ) [-12,0].
解析试题分析:(Ⅰ)点A代入圆C方程,
得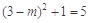 .
.
∵m<3,∴m=1. 2分
圆C: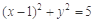 .设直线P
.设直线P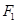 的斜率为k,
的斜率为k,
则PF1: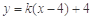 ,即
,即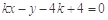 .
.
∵直线P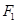 与圆C相切,∴
与圆C相切,∴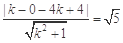 .
.
解得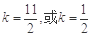 . 4分
. 4分
当k=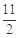 时,直线PF1与x轴的交点横坐标为
时,直线PF1与x轴的交点横坐标为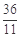 ,不合题意,舍去.
,不合题意,舍去.
当k=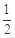 时,直线PF1与x轴的交点横坐标为-4,
时,直线PF1与x轴的交点横坐标为-4,
∴c=4.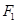 (-4,0),
(-4,0),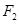 (4,0).
(4,0).
2a=A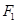 +A
+A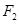 =
=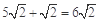 ,
,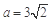 ,a2=18,b2=2.
,a2=18,b2=2.
椭圆E的方程为: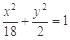 . 7分
. 7分
(Ⅱ)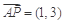 ,设Q(x,y),
,设Q(x,y), ,
,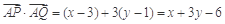 . 9分
. 9分
∵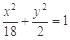 ,即
,即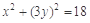 ,
,
而 ,∴-18≤6xy≤18.
,∴-18≤6xy≤18.
则 的取值范围是[0,36].
的取值范围是[0,36].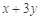 的取值范围是[-6,6].
的取值范围是[-6,6].
∴ 的取值范围是[-12,0]. 13分
的取值范围是[-12,0]. 13分
考点:本题主要考查直线方程,直线与圆的位置关系,椭圆标准方程,向量的坐标运算,基本不等式的应用。
点评:中档题,研究直线与圆的位置关系,半径、弦长一半、圆心到直线的距离所构成的“特征三角形”是重点,考查知识覆盖面广,对考生计算能力、数形结合思想有较好考查。

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
 的方程为
的方程为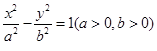 ,
,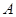 、
、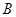 为其左、右两个顶点,
为其左、右两个顶点,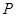 是双曲线
是双曲线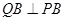 ,
,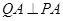 ,垂足分别为
,垂足分别为 与
与 交于点
交于点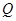 .
.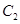 方程;
方程; 、
、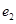 ,当
,当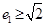 时,求
时,求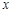 轴上,长轴长是短轴长的2倍的椭圆经过点M(2,1)
轴上,长轴长是短轴长的2倍的椭圆经过点M(2,1)  平行于
平行于 ,且与椭圆交于A、B两个不同点.
,且与椭圆交于A、B两个不同点.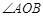 为钝角,求直线
为钝角,求直线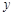 轴上的截距m的取值范围;
轴上的截距m的取值范围;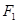
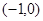 、
、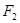
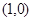 为椭圆的焦点,且直线
为椭圆的焦点,且直线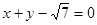 与椭圆相切.
与椭圆相切. 、
、 两点,求△
两点,求△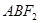 的面积
的面积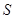 的最大值,并求此时直线的方程。
的最大值,并求此时直线的方程。 的顶点在坐标原点,它的准线经过双曲线
的顶点在坐标原点,它的准线经过双曲线 :
: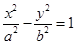 的一个焦点
的一个焦点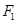 且垂直于
且垂直于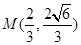 .
.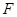 的坐标;
的坐标;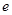 .
.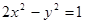 的右支交于不同的两点A,B.
的右支交于不同的两点A,B.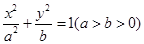 的左、右焦点分别为
的左、右焦点分别为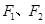 ,离心率
,离心率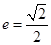 ,
, 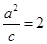 .
.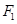 的直线
的直线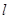 与该椭圆交于
与该椭圆交于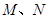 两点,且
两点,且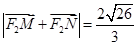 ,求直线
,求直线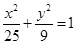 有相同的焦点,求此双曲线方程.
有相同的焦点,求此双曲线方程.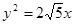 的焦点是双曲线C的一个焦点,且双曲线经过点
的焦点是双曲线C的一个焦点,且双曲线经过点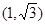 ,又知直线
,又知直线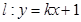 与双曲线C相交于A、B两点.
与双曲线C相交于A、B两点.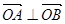 ,求实数k值.
,求实数k值.