题目内容
【题目】若关于x的不等式|x+a|≤b的解集为[﹣6,2].
(1)求实数a,b的值;
(2)若实数m,n满足|am+n|< ![]() ,|m﹣bn|<
,|m﹣bn|< ![]() ,求证:|n|<
,求证:|n|< ![]() .
.
【答案】
(1)解:关于x的不等式|x+a|≤b的解集为[﹣b﹣a,b﹣a],
∵关于x的不等式|x+a|≤b的解集为[﹣6,2],
∴ ![]() ,∴a=2,b=4
,∴a=2,b=4
(2)证明:∵实数m,n满足|am+n|< ![]() ,|m﹣bn|<
,|m﹣bn|< ![]() ,
,
∴|n|= ![]() |(2m+n)﹣(2m﹣8n)|≤
|(2m+n)﹣(2m﹣8n)|≤ ![]() |2m+n|+2|m﹣4n|<
|2m+n|+2|m﹣4n|< ![]() =
= ![]()
【解析】(1)关于x的不等式|x+a|≤b的解集为[﹣b﹣a,b﹣a],利用条件建立方程组,即可求实数a,b的值;(2)利用|n|= ![]() |(2m+n)﹣(2m﹣8n)|≤
|(2m+n)﹣(2m﹣8n)|≤ ![]() |2m+n|+2|m﹣4n|,即可证明结论.
|2m+n|+2|m﹣4n|,即可证明结论.
【考点精析】根据题目的已知条件,利用绝对值不等式的解法的相关知识可以得到问题的答案,需要掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.

 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案【题目】现采用随机模拟的方法估计某运动员射击4次,至少击中3次的概率:先由计算器给出0到9之间取整数值的随机数,指定0,1表示没有击中目标,2,3,4,5,6,7,8,
9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了20组随机数:
7527 | 0293 | 7140 | 9857 | 0347 | 4373 | 8636 | 6947 | 1417 | 4698 |
0371 | 6233 | 2616 | 8045 | 6011 | 3661 | 9597 | 7424 | 7610 | 4281 |
根据以上数据估计该射击运动员射击4次至少击中3次的概率为_______.
【题目】在统计学中,偏差是指个别测定值与测定的平均值之差,在成绩统计中,我们把某个同学的某科考试成绩与该科班平均分的差叫某科偏差,班主任为了了解个别学生的偏科情况,对学生数学偏差x(单位:分)与物理偏差y(单位:分)之间的关系进行学科偏差分析,决定从全班56位同学中随机抽取一个容量为8的样本进行分析,得到他们的两科成绩偏差数据如下:
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
数学偏差x | 20 | 15 | 13 | 3 | 2 | -5 | -10 | -18 |
物理偏差y | 6.5 | 3.5 | 3.5 | 1.5 | 0.5 | -0.5 | -2.5 | -3.5 |
(1)已知x与y之间具有线性相关关系,求y关于x的线性回归方程;
(2)若这次考试该班数学平均分为118分,物理平均分为90.5,试预测数学成绩126分的同学的物理成绩.
参考公式: 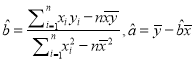 .
.
参考数据: ![]() .
.
【题目】某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
零件的个数x(个) | 2 | 3 | 4 | 5 |
加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出y关于x的线性回归方程![]() ;
;
(3)试预测加工10个零件需要多少时间.
参考公式:回归直线![]() ,
,
其中 ,
,![]()
【题目】已知函数f(x)的定义域为[﹣1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示,下列关于函数f(x)的命题:
x | ﹣1 | 0 | 4 | 5 |
f(x) | 1 | 2 | 2 | 1 |
(1)函数y=f(x)是周期函数;
(2)函数f(x)在(0,2)上是减函数;
(3)如果当x∈[﹣1,t]时,f(x)的最大值是2,那么t的最大值为4;
(4)当1<a<2时,函数y=f(x)﹣a有4个零点.
其中真命题的个数有( )
A.1个
B.2个
C.3个
D.4个
