题目内容
【题目】已知向量a=(x+z,3),b=(2,y-z),且a⊥b.若x,y满足不等式|x|+|y|≤1,则z的取值范围是__________.
【答案】[-3,3]
【解析】由a⊥b,得2(x+z)+3(y-z)=0,∴ z=2x+3y,由约束条件|x|+|y|≤1,画出平行域.由图可知z在(0,-1)和(0,1)时,分别取最小值-3和最大值3,故z∈[-3,3].
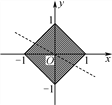
点晴:本题考查的是线性规划问题中最值问题,线性规划问题的实质是把代数问题几何化,即数形结合的思想,需要注意的是:一,准确无误地作出可行域;二,画目标函数所对应的直线时,要注意与约束条件中的直线的斜率进行比较,避免出错;三,一般情况下,目标函数的最值会在可行域的端点或边界上取得.

 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案【题目】某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数,得到如下资料:
日 期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
温差 | 10 | 11 | 13 | 12 | 8 |
发芽数 | 23 | 25 | 30 | 26 | 16 |
该农科所确定的研究方案是:先从这五组数据中选取2组,用剩下的3组数据求线性回归方程,再对被选取的2组数据进行检验.
(1)求选取的2组数据恰好是不相邻2天数据的概率;
(2)若选取的是12月1日与12月5日的两组数据,请根据12月2日至12月4日的数据,求出y关于x的线性回归方程![]() ;
;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?
(注: 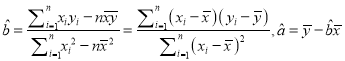 )
)
【题目】(本小题满分10分,第(1)问 5分,第(2)问 5 分)
近年来,微信越来越受欢迎,许多人通过微信表达自己、交流思想和传递信息,微信是现代生活中进行信息交流的重要工具.而微信支付为用户带来了全新的支付体验,支付环节由此变得简便而快捷.某商场随机对商场购物的![]() 名顾客进行统计,其中
名顾客进行统计,其中![]() 岁以下占
岁以下占![]() ,采用微信支付的占
,采用微信支付的占![]() ,
, ![]() 岁以上采用微信支付的占
岁以上采用微信支付的占![]() 。
。
(1)请完成下面![]() 列联表:
列联表:
|
| 合计 | |
使用微信支付 | |||
未使用微信支付 | |||
合计 |
(2)并由列联表中所得数据判断有多大的把握认为“使用微信支付与年龄有关”?
参考公式:  ,
, ![]() .
.
参考数据:
|
|
|
|
|
|
|
|
|
|
