题目内容
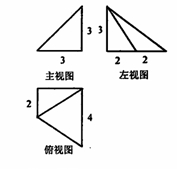
一个多面体的直观图和三视图如图所示,其中M,N分别是AB,AC的中点,G是DF上的一动点.


(1)求该多面体的体积与表面积;
(2)求证:GN⊥AC;
(3)当FG=GD时,在棱AD上确定一点P,使得GP∥平面FMC,并给出证明.


(1)求该多面体的体积与表面积;
(2)求证:GN⊥AC;
(3)当FG=GD时,在棱AD上确定一点P,使得GP∥平面FMC,并给出证明.
(1)(3+ )a2 (2)见解析 (3)见解析
)a2 (2)见解析 (3)见解析
 )a2 (2)见解析 (3)见解析
)a2 (2)见解析 (3)见解析解:(1)由题中图可知该多面体为直三棱柱,
在△ADF中,AD⊥DF,DF=AD=DC=a,
所以该多面体的体积为
 a3,
a3,表面积为
 a2×2+
a2×2+ a2+a2+a2=(3+
a2+a2+a2=(3+ )a2.
)a2.
(2)连接DB,FN,
由四边形ABCD为正方形,
且N为AC的中点知B,N,D三点共线,且AC⊥DN.
又∵FD⊥AD,FD⊥CD,AD∩CD=D,∴FD⊥平面ABCD.
∵AC?平面ABCD,
∴FD⊥AC.
又DN∩FD=D,
∴AC⊥平面FDN,
又GN?平面FDN,
∴GN⊥AC.
(3)点P与点A重合时,GP∥平面FMC.
取FC的中点H,连接GH,GA,MH.
∵G是DF的中点,∴GH

 CD.
CD.又M是AB的中点,∴AM

 CD.
CD.∴GH∥AM且GH=AM,
∴四边形GHMA是平行四边形.
∴GA∥MH.
∵MH?平面FMC,GA?平面FMC,
∴GA∥平面FMC,即当点P与点A重合时,GP∥平面FMC.

练习册系列答案
相关题目
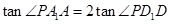 ,则点P的轨迹是( )
,则点P的轨迹是( )
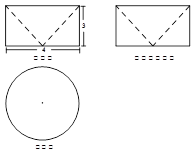
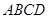 各棱长均相等,
各棱长均相等, 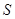 为
为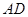 的中点,
的中点, 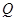 为
为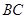 上异于中点和端点的任一点,则
上异于中点和端点的任一点,则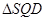 在四面体的面
在四面体的面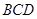 上的的射影可能是
上的的射影可能是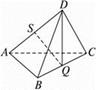
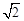 的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将表面积为
的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将表面积为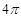 的鸡蛋(视为球体)放入其中,蛋巢形状保持不变, 则鸡蛋中心(球心)与蛋巢底面的距离为
的鸡蛋(视为球体)放入其中,蛋巢形状保持不变, 则鸡蛋中心(球心)与蛋巢底面的距离为





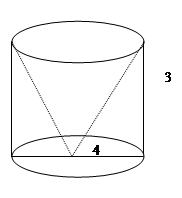
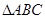 的直观图,
的直观图,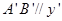 轴,
轴,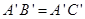 ,则
,则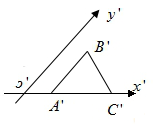
 A1B1C1D1中,M,N分别是BC1,CD1的中点,则下列判断错误的是( )
A1B1C1D1中,M,N分别是BC1,CD1的中点,则下列判断错误的是( )