题目内容
【题目】在直角坐标系![]() 中,斜率为k的动直线l过点
中,斜率为k的动直线l过点![]() ,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() .
.
(1)若直线l与曲线C有两个交点,求这两个交点的中点P的轨迹![]() 关于参数k的参数方程;
关于参数k的参数方程;
(2)在条件(1)下,求曲线![]() 的长度.
的长度.
【答案】(1)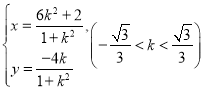 ;(2)
;(2)![]()
【解析】
(1)把![]() 两边同时乘以
两边同时乘以![]() ,然后结合极坐标与直角坐标的互化公式可得曲线
,然后结合极坐标与直角坐标的互化公式可得曲线![]() 的直角坐标方程,设直线
的直角坐标方程,设直线![]() 的方程为
的方程为![]() ,与曲线
,与曲线![]() 联立,利用根与系数的关系可得两个交点的中点
联立,利用根与系数的关系可得两个交点的中点![]() 的轨迹
的轨迹![]() 关于参数
关于参数![]() 的参数方程;
的参数方程;
(2)化参数方程为普通方程,作出图形,数形结合即可求得曲线![]() 的长度.
的长度.
解:(1)曲线C的直角坐标方程为![]() .
.
设直线l的方程为![]() ,
,
设直线l与曲线C的交点为![]() ,
,![]() ,
,
联立直线l与曲线C的方程得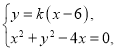
解得![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
设P的坐标为![]() ,则
,则![]() ,代入l的方程得
,代入l的方程得![]() .
.
故![]() 的参数方程为
的参数方程为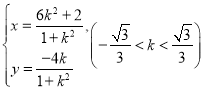 .
.
(2)由![]() 的参数方程
的参数方程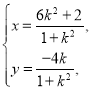 得
得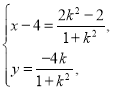 即
即![]() .
.
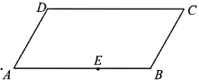
如图,圆C:圆心为![]() ,半径为2,
,半径为2,
圆D:圆心为![]() ,半径为2,曲线
,半径为2,曲线![]() 为劣弧
为劣弧![]() ,
,
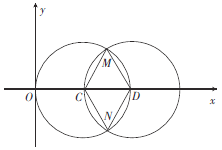
显然![]() ,
,
所以![]() 的长度为
的长度为![]() .
.

【题目】某市春节期间7家超市的广告费支出![]() (万元)和销售额
(万元)和销售额![]() (万元)数据如下:
(万元)数据如下:
超市 | A | B | C | D | E | F | G |
广告费支出 | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
销售额 | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
参数数据及公式:![]() ,
,![]() ,
,![]() ,
,![]() ,
,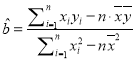 ,
,![]() ,
,![]() .
.
(1)若用线性回归模型拟合y与x的关系,求y关于x的线性回归方程;
(2)用对数回归模型拟合y与x的关系,可得回归方程:![]() ,经计算得出线性回归模型和对数模型的
,经计算得出线性回归模型和对数模型的![]() 分别约为0.75和0.97,请用
分别约为0.75和0.97,请用![]() 说明选择哪个回归模型更合适,并用此模型预测A超市广告费支出为8万元时的销售额.
说明选择哪个回归模型更合适,并用此模型预测A超市广告费支出为8万元时的销售额.
【题目】为了了解一个小水库中养殖的鱼的有关情况,从这个水库中多个不同位置捕捞出100条鱼,称得每条鱼的质量(单位:kg),并将所得数据分组,画出频率分布直方图(如图所示).
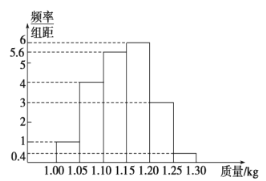
(1)在下面表格中填写相应的频率;
分组 | 频率 |
| |
| |
| |
| |
| |
|
(2)估计数据落在![]() 中的概率;
中的概率;
(3)将上面捕捞的100条鱼分别作一记分组频率号后再放回水库.几天后再从水库的多处不同位置捕捞出120条鱼,其中带有记号的鱼有6条.请根据这一情况来估计该水库中鱼的总条数.