题目内容
【题目】已知
、
是椭圆和双曲线的公共焦点，
是他们的一个公共点，且
，则椭圆和双曲线的离心率的倒数之和的最大值为___.
【答案】
【解析】
设|PF1|=r1，|PF2|=r2，|F1F2|=2c，椭圆和双曲线的离心率分别为e1，e2, 由余弦定理可得
4c2=（r1）2+（r2）2﹣2r1r2cos
，①在椭圆中，①化简为即4c2=4a2﹣3r1r2…②，在双曲线中，
化简为即4c2=4a12+r1r2…③，
，再利用柯西不等式求椭圆和双曲线的离
心率的倒数之和的最大值.
设椭圆的长半轴为a，双曲线的实半轴为a1，（a＞a1），半焦距为c，
由椭圆和双曲线的定义可知，
设|PF1|=r1，|PF2|=r2，|F1F2|=2c，
椭圆和双曲线的离心率分别为e1，e2,
∵∠F1PF2=，则∴由余弦定理可得4c2=（r1）2+（r2）2﹣2r1r2cos，①
在椭圆中，①化简为即4c2=4a2﹣3r1r2…②，
在双曲线中，①化简为即4c2=4a12+r1r2…③，
，
由柯西不等式得（1+
）（
）≥（
）2
故答案为：
教学练新同步练习系列答案
课前课后同步练习系列答案
课堂小作业系列答案
黄冈小状元口算速算练习册系列答案
成功训练计划系列答案
倍速训练法直通中考考点系列答案
【题目】若某产品的直径长与标准值的差的绝对值不超过1mm 时，则视为合格品，否则视为不合格品。在近期一次产品抽样检查中，从某厂生产的此种产品中，随机抽取5000件进行检测，结果发现有50件不合格品。计算这50件不合格品的直径长与标准值的差（单位：mm）, 将所得数据分组，得到如下频率分布表：
分组 | 频数 | 频率 |
[-3, -2) |
| 0.10 |
[-2, -1) | 8 |
|
（1,2] |
| 0.50 |
（2,3] | 10 |
|
（3,4] |
|
|
合计 | 50 | 1．00 |
（Ⅰ）将上面表格中缺少的数据填在答题卡的相应位置；
（Ⅱ）估计该厂生产的此种产品中，不合格品的直径长与标准值的差落在区间（1,3]内的概率；
（Ⅲ）现对该厂这种产品的某个批次进行检查，结果发现有20件不合格品。据此估算这批产品中的合格品的件数。
【题目】某种产品的质量按照其质量指标值M进行等级划分，具体如下表：
质量指标值M |
|
|
|
等级 | 三等品 | 二等品 | 一等品 |
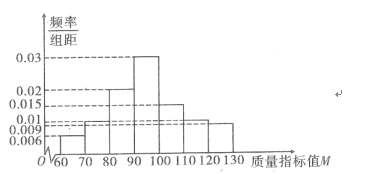
现从某企业生产的这种产品中随机抽取了100件作为样本，对其质量指标值M进行统计分析，得到如图所示的频率分布直方图.
（1）记A表示事件“一件这种产品为二等品或一等品”，试估计事件A的概率；
（2）已知该企业的这种产品每件一等品、二等品、三等品的利润分别为10元、6元、2元，试估计该企业销售10000件该产品的利润；
（3）根据该产品质量指标值M的频率分布直方图，求质量指标值M的中位数的估计值（精确到0.01）
