题目内容
【题目】古希腊著名数学家阿波罗尼斯与欧几里得、阿基米德齐名.他发现:“平面内到两个定点![]() 的距离之比为定值
的距离之比为定值![]() 的点的轨迹是圆”.后来,人们将这个圆以他的名字命名,称为阿波罗尼斯圆,简称阿氏圆在平面直角坐标系
的点的轨迹是圆”.后来,人们将这个圆以他的名字命名,称为阿波罗尼斯圆,简称阿氏圆在平面直角坐标系![]() 中,
中,![]() 点
点![]() .设点
.设点![]() 的轨迹为
的轨迹为![]() ,下列结论正确的是( )
,下列结论正确的是( )
A. ![]() 的方程为
的方程为![]()
B. 在![]() 轴上存在异于
轴上存在异于![]() 的两定点
的两定点![]() ,使得
,使得![]()
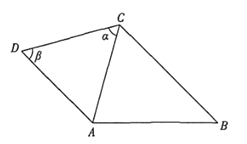
C. 当![]() 三点不共线时,射线
三点不共线时,射线![]() 是
是![]() 的平分线
的平分线
D. 在![]() 上存在点
上存在点![]() ,使得
,使得![]()
【答案】BC
【解析】
通过设出点P坐标,利用![]() 即可得到轨迹方程,找出两点
即可得到轨迹方程,找出两点![]() 即可判断B的正误,设出
即可判断B的正误,设出![]() 点坐标,利用
点坐标,利用![]() 与圆的方程表达式解出就存在,解不出就不存在.
与圆的方程表达式解出就存在,解不出就不存在.
设点![]() ,则
,则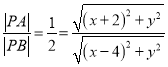 ,化简整理得
,化简整理得![]() ,即
,即![]() ,故A错误;当
,故A错误;当![]() 时,
时,![]() ,故B正确;对于C选项,
,故B正确;对于C选项,![]() ,
,![]() ,要证PO为角平分线,只需证明
,要证PO为角平分线,只需证明![]() ,即证
,即证![]() ,化简整理即证
,化简整理即证![]() ,设
,设![]() ,则
,则![]() ,
,
![]() ,则证
,则证
![]() ,故C正确;对于D选项,设
,故C正确;对于D选项,设![]() ,由
,由![]() 可得
可得![]() ,整理得
,整理得![]() ,而点M在圆上,故满足
,而点M在圆上,故满足![]() ,联立解得
,联立解得![]() ,
,![]() 无实数解,于是D错误.故答案为BC.
无实数解,于是D错误.故答案为BC.

练习册系列答案
相关题目
【题目】某工厂为了对研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价 | 9 | 9.2 | 9.4 | 9.6 | 9.8 | 10 |
销量 | 100 | 94 | 93 | 90 | 85 | 78 |
(1)若销量![]() 与单价
与单价![]() 服从线性相关关系,求该回归方程;
服从线性相关关系,求该回归方程;
(2)在(1)的前提下,若该产品的成本是5元/件,问:产品该如何确定单价,可使工厂获得最大利润。
附:对于一组数据![]() ,
,![]() ,……
,……![]() ,
,
其回归直线![]() 的斜率的最小二乘估计值为
的斜率的最小二乘估计值为 ;
;
本题参考数值:![]() .
.