题目内容
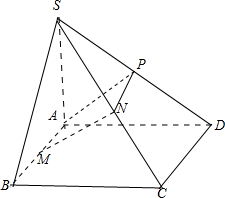
已知四棱锥S-ABCD,底面为正方形,SA⊥底面ABCD,AB=AS=a,M、N分别为AB、SC中点.
(Ⅰ)求四棱锥S-ABCD的表面积;
(Ⅱ)求证:MN∥平面SAD.

(Ⅰ)求四棱锥S-ABCD的表面积;
(Ⅱ)求证:MN∥平面SAD.

(Ⅰ)∵SA⊥底面ABCD,∴SA⊥AB,SA⊥AD,SA⊥BC.
又BC⊥AB,∴BC⊥平面SAB,∴BC⊥SB,同理,CD⊥SD,(3分)
∴△SAB≌△SAD,△SBC≌△SCD.
又∵SB=
a,∴S表面积=2S△SAB+2S△SBC+SABCD
=2×
a2+2×
a•
a+a2=(2+
)a2.(7分)
(Ⅱ)取SD中点P,连接MN、NP、PA,则NP=
CD,且NP∥CD.(9分)
又AM=
CD,且AM∥CD,∴NP=AM,NP∥AM,∴AMNP是平行四边形.(12分)
∴MN∥AP,而AP?平面SAD,MN不在平面SAD内,∴MN∥平面SAD.(14分)
又BC⊥AB,∴BC⊥平面SAB,∴BC⊥SB,同理,CD⊥SD,(3分)
∴△SAB≌△SAD,△SBC≌△SCD.
又∵SB=
| 2 |
=2×
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
(Ⅱ)取SD中点P,连接MN、NP、PA,则NP=
| 1 |
| 2 |
又AM=
| 1 |
| 2 |
∴MN∥AP,而AP?平面SAD,MN不在平面SAD内,∴MN∥平面SAD.(14分)


练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案
相关题目