题目内容
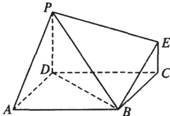
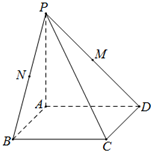
如图,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是侧棱PA上的动点.
(I)求四棱锥P-ABCD的体积;
(Ⅱ)如果E是PA的中点,求证:PC∥平面BDE;
(Ⅲ)探究:不论点E在侧棱PA的任何位置,BD⊥CE是否都成立?若成立,证明你的结论;若不成立,请说明理由.

(I)求四棱锥P-ABCD的体积;
(Ⅱ)如果E是PA的中点,求证:PC∥平面BDE;
(Ⅲ)探究:不论点E在侧棱PA的任何位置,BD⊥CE是否都成立?若成立,证明你的结论;若不成立,请说明理由.

(1)∵PA⊥平面ABCD,
∴VP-ABCD=
SABCD•PA=
×12×2=
…3分
即四棱锥P-ABCD的体积为
.…4分
(2)证明:连接AC交BD于O,连接OE.
∵四边形ABCD是正方形,∴O是AC的中点.
又∵E是PA的中点,∴PC∥OE.…6分
∵PC?平面BDE,OE?平面BDE
∴PC∥平面BDE.…8分
(3)不论点E在何位置,BD⊥CE成立.…9分
证明如下:∵四边形ABCD是正方形,∴BD⊥AC.
∵PA⊥平面ABCD,且BD?平面ABCD,∴BD⊥PA.
又∵AC∩PA=A,∴BD⊥平面PAC.…10分
∵不论点E在何位置,都有CE?平面PAC.
∴不论点点E在何位置,BD⊥CE成立.…12分.

∴VP-ABCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
即四棱锥P-ABCD的体积为
| 2 |
| 3 |
(2)证明:连接AC交BD于O,连接OE.
∵四边形ABCD是正方形,∴O是AC的中点.
又∵E是PA的中点,∴PC∥OE.…6分
∵PC?平面BDE,OE?平面BDE
∴PC∥平面BDE.…8分
(3)不论点E在何位置,BD⊥CE成立.…9分
证明如下:∵四边形ABCD是正方形,∴BD⊥AC.
∵PA⊥平面ABCD,且BD?平面ABCD,∴BD⊥PA.
又∵AC∩PA=A,∴BD⊥平面PAC.…10分
∵不论点E在何位置,都有CE?平面PAC.
∴不论点点E在何位置,BD⊥CE成立.…12分.


练习册系列答案
相关题目