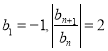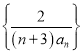题目内容
【题目】在平面直角坐标系
中，对于点
，若函数
满足：
，都有
，就称这个函数是点A的“限定函数”.以下函数：①
，②
，③
，④
，其中是原点O的“限定函数”的序号是______.已知点在函数
的图象上，若函数是点A的“限定函数”，则实数a的取值范围是______.
【答案】①③ 
【解析】
(1)当
，求出各序号中y的取值范围A，若
则此函数是原点的“限定函数”； (2) 由题意知
，当
时
，若
是点A的“限定函数”，则
，由集合的包含关系列出不等式组即可求得a的取值范围.
(1) ①当时，
，因为
，所以函数①是原点的“限定函数”；
②因为
在
上单调递减，在
上单调递增，所以当时， 
，因为
，所以②不是原点的“限定函数”；
③因为
在
上单调递增，所以当时，
，因为
，所以③是原点的“限定函数”；
④因为
在
上单调递增，所以当时，
，因为
，所以④不是原点的“限定函数”.
(2)因为点
在函数的图象上，所以，
因为是点A的“限定函数”，并且当时，，
所以
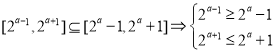，解得.
故答案为：①③；
练习册系列答案
相关题目
