题目内容
20.已知过点P(-2,0)的双曲线C与椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1有相同的焦点,则双曲线C的渐近线方程是y=$±\sqrt{3}x$.分析 通过椭圆方程可知双曲线焦点F1(-4,0)、F2(4,0),并利用点P在双曲线上,计算即得结论.
解答 解:依题意,椭圆焦点F1(-4,0),F2(4,0),
设双曲线方程:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1,
则$\left\{\begin{array}{l}{\frac{(-2)^{2}}{{a}^{2}}-\frac{0}{{b}^{2}}=1}\\{{a}^{2}+{b}^{2}={4}^{2}}\end{array}\right.$,
解得:a=2,b=$2\sqrt{3}$,
∴双曲线方程为:$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=0,
∴其渐近线方程为:y=±$\frac{2\sqrt{3}}{2}$x=$±\sqrt{3}x$,
故答案为:y=$±\sqrt{3}x$.
点评 本题考查椭圆的简单性质,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
10.在某地人们发现某种蟋蟀1min所叫次数与当地气温之间近似为一次函数,下面是蟋蟀所叫次数与气温变化情况对照表:
(1)根据表中数据确定该一次函数的关系式;
(2)如果蟋蟀1min叫了63次,那么该地当时的温度大约为多少摄氏度;
(3)能用所求的函数模型来预测蟋蟀在0℃时所鸣叫的次数.
| 蟋蟀叫次数 | … | 84 | 98 | 119 | … |
| 温度(℃) | … | 15 | 17 | 20 | … |
(2)如果蟋蟀1min叫了63次,那么该地当时的温度大约为多少摄氏度;
(3)能用所求的函数模型来预测蟋蟀在0℃时所鸣叫的次数.
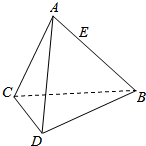 如图,棱长为4的正四面体ABCD,AE=$\frac{1}{3}$AB,试建立适当的坐标系,写出各点的坐标.
如图,棱长为4的正四面体ABCD,AE=$\frac{1}{3}$AB,试建立适当的坐标系,写出各点的坐标.