题目内容
在三棱锥S-ABC中,如图,∠SAB=∠SAC=∠ACB=90°,AC=2,
BC=
,SB=
.
(1)证明:SC⊥BC;
(2)求侧面SBC与底面ABC所成的二面角大小;
(3)(理)求异面直线SC与AB所成的角的大小(用反三角函数表示).
(文)求三棱锥的体积VS-ABC.
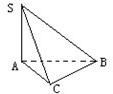
BC=
| 13 |
| 29 |
(1)证明:SC⊥BC;
(2)求侧面SBC与底面ABC所成的二面角大小;
(3)(理)求异面直线SC与AB所成的角的大小(用反三角函数表示).
(文)求三棱锥的体积VS-ABC.

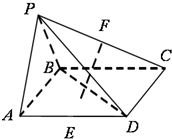
(1)证明:如图,
∵∠SAB=∠SAC=90°
∴SA⊥底面ACB
又∵BC?底面ACB
∴SA⊥BC
又∵∠ACB=90°
∴AC⊥BC
又∵SA∩AC=A
∴BC⊥面ASC
又∵SC?面ASC
∴SC⊥BC
(2)∵∠ACB=90°
∴AC⊥BC
又∵SC⊥BC
∴∠SCA即为侧面SBC与底面ABC所成的二面角的平面角
在Rt△ACB中,AC=2,BC=
,∴AB=
在Rt△SAB中,AB=
,SB=
,∴SA=2
在Rt△SAC中,SA=2
,AC=2,∴∠SCA=60°,
即侧面SBC与底面ABC所成的二面角的大小为60°
(3)
(理)分别取AC、SB、CB、SC的中点D、E、F、M,连接DE、EF、DF、ME、MD,则:ME∥CB,EF∥SC,DF∥AB,
所以异面直线SC与AB所成的角的大小即为∠EFD的大小.
∵ME∥CB,BC⊥面ASC
∴ME⊥面ASC
∴ME⊥MD,又ME=
,MD=
,则ED=
又∵EF=2,DF=
∴cos∠EFD=
=
∴异面直线SC与AB所成的角的大小为arccos
.
(文)∵S△ACB=
AC•BC=
,SA=2
,
∴VS-ABC=
•
•2
=
.
∵∠SAB=∠SAC=90°
∴SA⊥底面ACB
又∵BC?底面ACB
∴SA⊥BC
又∵∠ACB=90°
∴AC⊥BC
又∵SA∩AC=A
∴BC⊥面ASC
又∵SC?面ASC
∴SC⊥BC
(2)∵∠ACB=90°
∴AC⊥BC
又∵SC⊥BC
∴∠SCA即为侧面SBC与底面ABC所成的二面角的平面角
在Rt△ACB中,AC=2,BC=
| 13 |
| 17 |
在Rt△SAB中,AB=
| 17 |
| 29 |
| 3 |
在Rt△SAC中,SA=2
| 3 |
即侧面SBC与底面ABC所成的二面角的大小为60°
(3)
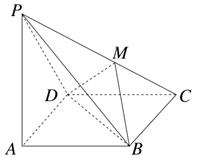
(理)分别取AC、SB、CB、SC的中点D、E、F、M,连接DE、EF、DF、ME、MD,则:ME∥CB,EF∥SC,DF∥AB,
所以异面直线SC与AB所成的角的大小即为∠EFD的大小.
∵ME∥CB,BC⊥面ASC
∴ME⊥面ASC
∴ME⊥MD,又ME=
| ||
| 2 |
| 3 |
| 5 |
| 2 |
又∵EF=2,DF=
| ||
| 2 |
∴cos∠EFD=
| EF2+DF2-ED2 |
| 2EF•DF |
| ||
| 17 |
∴异面直线SC与AB所成的角的大小为arccos
| ||
| 17 |
(文)∵S△ACB=
| 1 |
| 2 |
| 13 |
| 3 |
∴VS-ABC=
| 1 |
| 3 |
| 13 |
| 3 |
2
| ||
| 3 |

练习册系列答案
 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目