题目内容
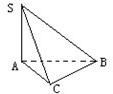
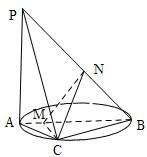
如图,AB是圆的直径,PA垂直圆所在的平面,C是圆上的点.
(Ⅰ)求证:平面PAC⊥平面PBC;
(Ⅱ)若AB=2,AC=1,PA=1,求证:二面角C-PB-A的余弦值.

(Ⅰ)求证:平面PAC⊥平面PBC;
(Ⅱ)若AB=2,AC=1,PA=1,求证:二面角C-PB-A的余弦值.

(Ⅰ)证明:如图,
由AB是圆的直径,得AC⊥BC.
由PA⊥平面ABC,BC?平面ABC,得PA⊥BC.
又PA∩AC=A,PA?平面APC,AC?平面PAC,
所以BC⊥平面PAC.
因为BC?平面PBC,
所以平面PAC⊥平面PBC;
(Ⅱ)过C作CM⊥AB于M,
因为PA⊥平面ABC,CM?平面ABC,所以PA⊥CM,
故CM⊥平面PAB.
过M作MN⊥PB于N,链接NC.
由三垂线定理得CN⊥PB.
所以∠CNM为二面角C-PB-A的平面角.
在Rt△ABC中,由AB=2,AC=1,得BC=
,CM=
,BM=
.
在Rt△ABP中,由AB=2,AP=1,得PB=
.
因为Rt△BNM∽Rt△BAP,所以
=
.
故MN=
.
又在Rt△CNM中,CN=
.故cos∠CNM=
.
所以二面角C-PB-A的余弦值为
.
由AB是圆的直径,得AC⊥BC.
由PA⊥平面ABC,BC?平面ABC,得PA⊥BC.
又PA∩AC=A,PA?平面APC,AC?平面PAC,
所以BC⊥平面PAC.
因为BC?平面PBC,
所以平面PAC⊥平面PBC;
(Ⅱ)过C作CM⊥AB于M,
因为PA⊥平面ABC,CM?平面ABC,所以PA⊥CM,
故CM⊥平面PAB.
过M作MN⊥PB于N,链接NC.
由三垂线定理得CN⊥PB.
所以∠CNM为二面角C-PB-A的平面角.
在Rt△ABC中,由AB=2,AC=1,得BC=
| 3 |
| ||
| 2 |
| 3 |
| 2 |
在Rt△ABP中,由AB=2,AP=1,得PB=
| 5 |
因为Rt△BNM∽Rt△BAP,所以
| MN |
| 1 |
| ||
|
故MN=
3
| ||
| 10 |
又在Rt△CNM中,CN=
| ||
| 5 |
| ||
| 4 |
所以二面角C-PB-A的余弦值为
| ||
| 4 |


练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目