Question

【题目】如图，在四棱锥P﹣ABCD中，PD⊥平面ABCD，AB∥CD，∠BAD=90°，AD= ，DC=2AB=2，E为BC中点．

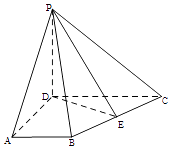
（1）求证：平面PBC⊥平面PDE
（2）线段PC上是否存在一点F，使PA∥平面BDF？若存在，求 的值；若不存在，说明理由．

Answer 1

【答案】
（1）证明：连接BD

在RT△DAB中，BD= =

知△DBC是等腰三角形．

又∵E为BC的中点．

∴DE⊥BC

∵PD⊥平面ABCD，且BC平面ABCD

∴PD⊥BC

∵PD∩DE=D

∴BC⊥平面PDE

又∵BC平面PBC

∴平面PBC⊥平面PDE

（2）解：线段PC上存在一点F，且 时，有PA∥平面BDF

证明如下：

连接AC交BD于点O，在平面PAC中过点O作OF∥PA，则交PC于F

又∵OF平面BDF，PA平面BDF

∴PA∥平面BDF

∵四边形ABCD中AB∥CD，

∴易知△ABO∽△CDO

又∵CD=2AB=2，

∴

∵OF∥PA

∴

∴当 时，PA∥平面BDF

【解析】（1）要证平面PBC⊥平面PDE，只要证平面PBC内的直线BC⊥平面PDE即可．（2）由线面平行的性质定理，若使PA∥平面BDF，则过直线PA的平面和平面BDF的交线会和PA平行，故作辅助线OF∥AP，再利用线面平行判定定理证明．确定F的位置，则利用三角形相似的相似比确定 的值．
【考点精析】本题主要考查了直线与平面平行的判定和平面与平面垂直的判定的相关知识点，需要掌握平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行；一个平面过另一个平面的垂线，则这两个平面垂直才能正确解答此题．