题目内容
已知{an}是公差不为零的等差数列,a1=1,且a1,a3,a9成等比数列.
(Ⅰ)求数列{an}的通项; (Ⅱ)求数列{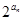 }的前n项和Sn.
}的前n项和Sn.
(1)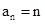 (2)
(2)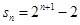 。
。
解析试题分析:(I)设公差为d,则a3=1+2d,a9=1+8d,所以,(1+2d)²=1(1+8d),
解得,d=1(d=0舍去),则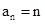 ;
;
(II)令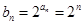 ,则由等比数列的求和公式
,则由等比数列的求和公式 ,得,
,得,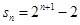
考点:等差数列、等比数列的通项公式及其求和公式。
点评:简单题,利用已知条件,建立公差的方程,较方便的得到等差数列的通项公式,从而进一步得到数列{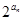 }的前n项和Sn
}的前n项和Sn

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 的前
的前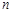 项和为
项和为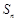 满足
满足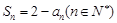 .
.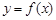 与函数
与函数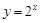 互为反函数,令
互为反函数,令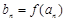 ,求数列
,求数列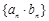 的前
的前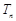 ;
;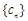 满足
满足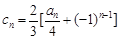 ,证明:对任意的整数
,证明:对任意的整数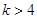 ,有
,有 .
.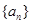 的前
的前 项和
项和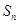 ,满足:
,满足: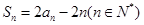 .
.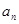 ;
;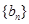 的满足
的满足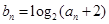 ,
,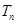 为数列
为数列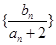 的前
的前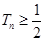 .
.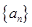 的前n项和为
的前n项和为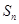 ,点
,点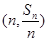 在直线
在直线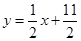 上.数列{bn}满足
上.数列{bn}满足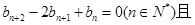
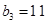 ,前9项和为153.
,前9项和为153.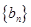 的通项公式;
的通项公式;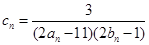 ,数列
,数列 的前n和为
的前n和为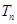 ,求使不等式
,求使不等式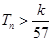 对一切
对一切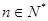 都成立的最大正整数k的值.
都成立的最大正整数k的值.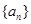 的前n项和为
的前n项和为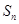 ,已知
,已知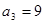 ,
, 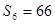 .
.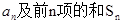 ;
;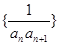 的前n项和为
的前n项和为 ,证明:
,证明: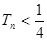 ;
; 满足
满足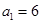 ,
,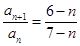
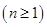 ;
;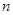 项和
项和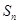 ,并求当
,并求当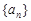 满足:
满足: ,数列
,数列 满足
满足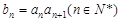 .
.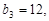 求
求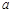 的值及
的值及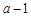 的等比数列,问是否存在正实数
的等比数列,问是否存在正实数 ,使得数列
,使得数列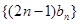 的前
的前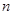 项和
项和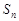 (用n,
(用n,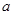 表示).
表示). 的前
的前 项和为
项和为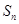 ,且
,且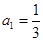 ,
,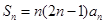
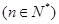 .
. 的值;
的值;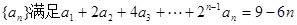 .
.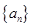 的通项公式;
的通项公式;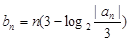 ,探求使
,探求使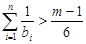 恒成立的
恒成立的 的最大整数值.
的最大整数值.