已知函数f(x)=$\left\{\begin{array}{l}{e}^{x}-2\\x+2a\end{array}\right.\begin{array}{c}x≤0\\.x＞0\end{array}\right.$对任意x1≠x2.都有$\frac{{f}}{{{x 1}-{x 2}}}$＞0成立.则实数a的取值范围是．[$-\frac{1}{2}.\frac{1}{2}$)� 题目和参考答案——青夏教育精英家教网——

题目内容

5．已知函数f（x）=$\left\{\begin{array}{l}{e}^{x}-2\\（1-2a）x+2a\end{array}\right.\begin{array}{c}x≤0\\，x＞0\end{array}\right.$对任意x₁≠x₂，都有$\frac{{f（{x_1}）-f（{x_2}）}}{{{x_1}-{x_2}}}$＞0成立，则实数a的取值范围是．[$-\frac{1}{2}，\frac{1}{2}$）．

分析根据已知条件便知函数f（x）在R上为增函数，从而x≤0，和x＞0时，f（x）都应为增函数，从而得到$a＜\frac{1}{2}$，并且有e⁰-2a≤（1-2a）•0+2a，从而1-2a≤2a，解该不等式与前面a的范围求交集即可得出实数a的取值范围．

解答解：由题意知函数f（x）在R上单调递增；
∴f（x）的两段函数在各自区间上单调递增；
∴1-2a＞0，即$a＜\frac{1}{2}$；
又e⁰-2≤（1-2a）•0+2a；
∴-1≤2a；
∴$a≥-\frac{1}{2}$；
∴实数a的取值范围是[$-\frac{1}{2}，\frac{1}{2}$）．
故答案为：[$-\frac{1}{2}，\frac{1}{2}$）．

点评考查增函数的定义，分段函数的单调性的判断方法，以及指数函数、一次函数的单调性，要掌握分段函数为单调函数时应满足的条件．

练习册系列答案

新思维冲刺小升初达标总复习系列答案

课时练优选卷系列答案

金榜小状元系列答案

单元自测题同步达标测试卷系列答案

小考练兵场系列答案

创新设计高考总复习系列答案

魔法教程课本诠释与思维拓展训练系列答案

北京市小学毕业考试考试说明系列答案

晨读晚练系列答案

小学毕业考试试卷精编系列答案

相关题目

15．过点（0，8）作曲线f（x）=x³-6x²+9x的切线，则这样的切线条数为（　　）

16．在△ABC中，2asinA=（2sinB-$\sqrt{3}$sinC）b+（2sinC-$\sqrt{3}$sinB）c．
（1）求∠A；
（2）若a=2，b=2$\sqrt{3}$，求△ABC的面积．

13．如图的框图表示的算法的功能是（　　）

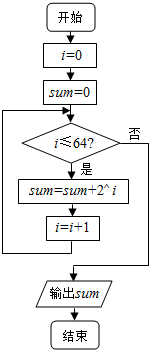
	A．	求和S=2+2²+…+2⁶⁴		B．	求和S=1+2+2²+…+2⁶³
	C．	求和S=1+2+2²+…+2⁶⁴		D．	以上均不对

20．下列图象中，有一个是函数$f（x）=\frac{1}{3}{x^3}+a{x^2}+（{a^2}-1）x+1（a∈$R，a≠0）的导函数f′（x）的图象，则f（-1）=-$\frac{1}{3}$
A、

10．命题“?x₀∈R，2${\;}^{{x}_{0}}$≥1”的否定是（　　）

?x₀∈R，2${\;}^{{x}_{0}}$＜1

?x₀∈R，2${\;}^{{x}_{0}}$≤1

?x∈R，2^x≥1

?x∈R，^x＜1

17．函数f（x）=2x-sinx在（-∞，+∞）上（　　）

14．已知{a_n}为等差数列，且满足a₁+a₃=8，a₂+a₄=12．
（Ⅰ）求数列{a_n}的通项公式；
（Ⅱ）记{a_n}的前n项和为S_n，若a₃，a_k+1，S_k成等比数列，求正整数k的值．

15．已知点A（a，a）（a≠0），B（1，0），O为坐标原点．若点C在直线OA上，且BC与OA垂直，则点C的坐标是（　　）

$（\frac{1}{2}，\;-\frac{1}{2}）$

$（\frac{a}{2}，\;-\frac{a}{2}）$

$（\frac{a}{2}，\;\frac{a}{2}）$

$（\frac{1}{2}，\;\frac{1}{2}）$