题目内容
17.某工厂有工人500名,记35岁以上(含35岁)的为A类工人,不足35岁的为B类工人,为调查该厂工人的个人文化素质状况,现用分层抽样的方法从A、B两类工人中分别抽取了40人、60人进行测试.(I)求该工厂A、B两类工人各有多少人?
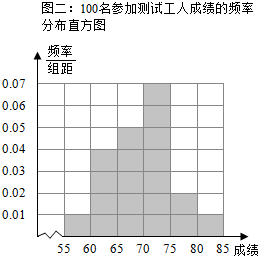
(Ⅱ)经过测试,得到以下三个数据图表:(茎、叶分别是十位和个位上的数字)(如图)
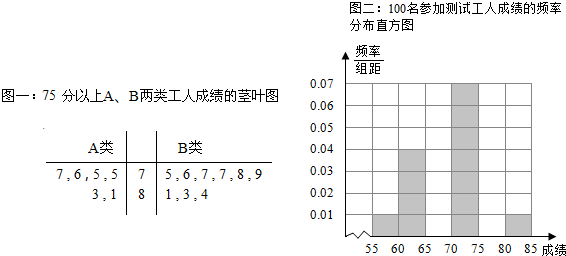
表:100名参加测试工人成绩频率分布表
| 组号 | 分组 | 频数 | 频率 |
| 1 | [55,60) | 5 | 0.05 |
| 2 | [60,65) | 20 | 0.20 |
| 3 | [65,70) | ||
| 4 | [70,75) | 35 | 0.35 |
| 5 | [75,80) | ||
| 6 | [80,85) | ||
| 合计 | 100 | 1.00 | |
②该厂拟定从参加考试的79分以上(含79分)的B类工人中随机抽取2人参加高级技工培训班,求抽到的2人分数都在80分以上的概率.
分析 (Ⅰ)根据分层抽样即可求出A,B类工人;
(Ⅱ)①根据茎叶图即可完成频率分布表和频率分布直方图;
②79分以上的B类工人共4人,记80分以上的三人分别为甲,乙,丙,79分的工人为a,一一列举出所有的基本事件,找到满足条件恩对基本事件,根据概率公式计算即可.
解答 解:(I)有题知A类工人有500×$\frac{40}{40+60}$=200(人);
则B类工人有500-200=300(人).
(Ⅱ)①表一,
| 组号 | 分组 | 频数 | 频率 |
| 1 | [55,60) | 5 | 0.05 |
| 2 | [60,65) | 20 | 0.20 |
| 3 | [65,70) | 25 | 0.25 |
| 4 | [70,75) | 35 | 0.35 |
| 5 | [75,80) | 10 | 0.10 |
| 6 | [80,85) | 5 | 0.05 |
| 合计 | 100 | 1.00 | |
②79分以上的B类工人共4人,记80分以上的三人分别为甲,乙,丙,79分的工人为a,
从中抽取2人,有(甲,乙),(甲,丙),(甲,a),(乙,丙),(乙,a),(丙,a)共6种抽法,
抽到2人均在80分以上有(甲,乙),(甲,丙),(乙,丙),共3种抽法.
则抽到2人均在80分以上的概率为$\frac{3}{6}$=$\frac{1}{2}$.
点评 本题考查了分层抽样,茎叶图,频率分布直方图,古典概率等知识,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.下面的程序框图表示算法的运行结果是( )
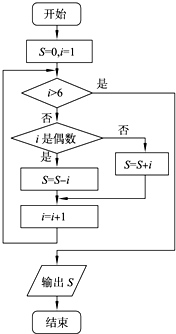

| A. | -3 | B. | -21 | C. | 3 | D. | 21 |
9.公差不为0的等差数列{an},其前23项和等于其前10项和,a8+ak=0,则正整数k=( )
| A. | 24 | B. | 25 | C. | 26 | D. | 27 |
5.已知圆M:x2+y2+2mx-3=0(m<0)的半径为2,则椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{3}$=1(a>0)的左焦点为F(-x,0),若垂直于x轴且经过F点的直线l与圆M相切,则a的值为( )
| A. | 2或2$\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 2 | D. | 4 |
