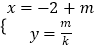题目内容
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为梯形,AD∥BC,AB=BC=CD=1,DA=2,DP⊥平面ABP,O,M分别是AD,PB的中点. 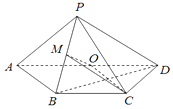
(Ⅰ)求证:PD∥平面OCM;
(Ⅱ)若AP与平面PBD所成的角为60°,求线段PB的长.
【答案】解:(Ⅰ)连接BD交OC与N,连接MN.
因为O为AD的中点,AD=2,
所以OA=OD=1=BC.
又因为AD∥BC,
所以四边形OBCD为平行四边形,
所以N为BD的中点,因为M为PB的中点,
所以MN∥PD.
又因为MN平面OCM,PD平面OCM,
所以PD∥平面OCM.
(Ⅱ)由四边形OBCD为平行四边形,知OB=CD=1,
所以△AOB为等边三角形,所以∠A=60°,
所以 ![]() ,即AB2+BD2=AD2,即AB⊥BD.
,即AB2+BD2=AD2,即AB⊥BD.
因为DP⊥平面ABP,所以AB⊥PD.
又因为BD∩PD=D,所以AB⊥平面BDP,
所以∠APB为AP与平面PBD所成的角,即∠APB=60°,
所以 ![]() .
.

【解析】(Ⅰ)连接BD交OC与N,连接MN.证明MN∥PD.然后证明PD∥平面OCM.(Ⅱ)通过计算证明AB⊥BD.AB⊥PD.推出AB⊥平面BDP,说明∠APB为AP与平面PBD所成的角,然后求解即可.
【考点精析】通过灵活运用直线与平面平行的判定和空间角的异面直线所成的角,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 即可以解答此题.
即可以解答此题.

 巧学巧练系列答案
巧学巧练系列答案【题目】某校为评估新教改对教学的影响,挑选了水平相当的两个平行班进行对比实验.甲班采用创新教法,乙班仍采用传统教法,一段时间后进行水平测试,成绩结果全部落在[60,100]区间内(满分100分),并绘制频率分布直方图如图,两个班人数均为60人,成绩80分及以上为优良. 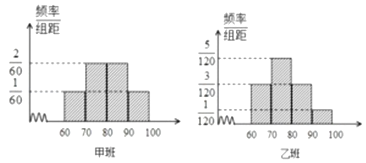
(1)根据以上信息填好2×2联表,并判断出有多大的把握认为学生
(2)成绩优良与班级有关?
(3)以班级分层抽样,抽取成绩优良的5人参加座谈,现从5人中随机选3人来作书面发言,求发言人至少有2人来自甲班的概率.(以下临界值及公式仅供参考)
P(k2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
k2= ![]() ,n=a+b+c+d.
,n=a+b+c+d.