题目内容
(本题满分12分)数列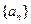 满足
满足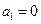 ,
,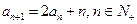 .
.
(1)设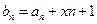 ,是否存在实数
,是否存在实数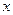 ,使得
,使得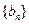 是等比数列;
是等比数列;
(2)是否存在不小于2的正整数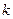 ,使得
,使得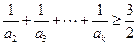 成立?若存在,求出
成立?若存在,求出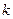 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由.
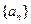 满足
满足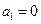 ,
,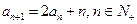 .
.(1)设
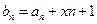 ,是否存在实数
,是否存在实数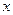 ,使得
,使得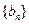 是等比数列;
是等比数列;(2)是否存在不小于2的正整数
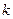 ,使得
,使得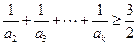 成立?若存在,求出
成立?若存在,求出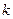 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由.解:(1)如果存在实数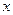 满足条件,则由已知得
满足条件,则由已知得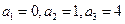 ,
,
所以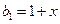 ,
,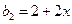 ,
,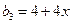 。
。
又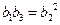 ,所以
,所以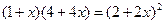 ,解得
,解得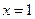 或
或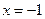 。….2分
。….2分
经检验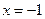 不合题意,舍去;
不合题意,舍去;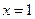 适合题意,可得
适合题意,可得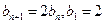 。
。
此时数列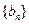 是等比数列,所以存在实数
是等比数列,所以存在实数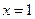 使得数列
使得数列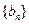 是等比数列。…..4分
是等比数列。…..4分
(2)由上面可得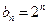 ,所以
,所以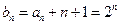 ,所以
,所以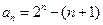 。….6分
。….6分
先证明,当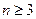 时,
时,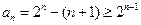 ,用数学归纳法
,用数学归纳法
①当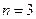 时,
时,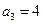 ,
,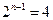 ,所以
,所以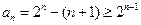 成立;
成立;
②假设当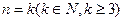 时,
时,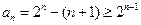 成立,即
成立,即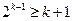 ,
,
则当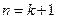 时,
时,
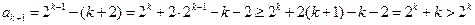
即当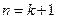 时,
时,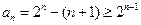 也成立.
也成立.
由①②可得,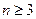 时,
时,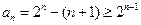 恒成立
恒成立
所以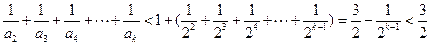 …11分
…11分
即不存在适合题设条件的正整数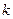 。
。
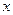 满足条件,则由已知得
满足条件,则由已知得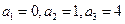 ,
,所以
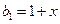 ,
,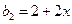 ,
,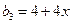 。
。又
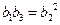 ,所以
,所以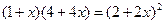 ,解得
,解得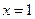 或
或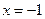 。….2分
。….2分经检验
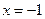 不合题意,舍去;
不合题意,舍去;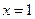 适合题意,可得
适合题意,可得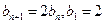 。
。此时数列
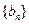 是等比数列,所以存在实数
是等比数列,所以存在实数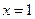 使得数列
使得数列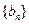 是等比数列。…..4分
是等比数列。…..4分(2)由上面可得
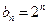 ,所以
,所以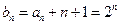 ,所以
,所以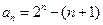 。….6分
。….6分先证明,当
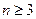 时,
时,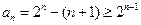 ,用数学归纳法
,用数学归纳法①当
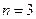 时,
时,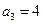 ,
,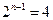 ,所以
,所以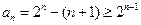 成立;
成立;②假设当
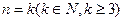 时,
时,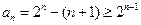 成立,即
成立,即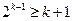 ,
,则当
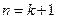 时,
时,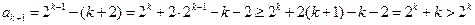
即当
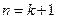 时,
时,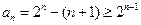 也成立.
也成立.由①②可得,
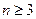 时,
时,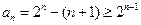 恒成立
恒成立所以
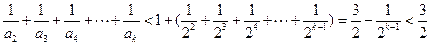 …11分
…11分即不存在适合题设条件的正整数
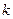 。
。略

练习册系列答案
相关题目
 和
和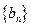 ,对一切正整数n都有:
,对一切正整数n都有: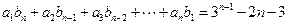 成立.
成立.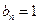 ,求数列
,求数列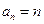 ,求证数列
,求证数列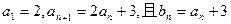 ,
,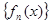 满足:
满足: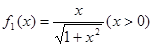 ,
,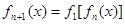
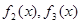 ;
;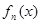 的表达式,并证明你的结论.
的表达式,并证明你的结论.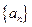 的首项
的首项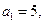 前
前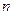 项和为
项和为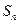 ,且
,且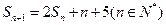
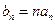 ,求数列
,求数列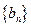 的前n项和
的前n项和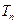 .
. 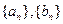 满足
满足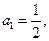
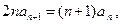 且
且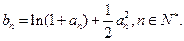
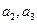 ,
,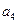 并求数列
并求数列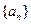 的通项公式;
的通项公式;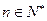 ,证明
,证明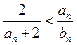 成立;
成立;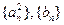 的前
的前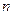 项和分别是
项和分别是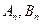 ,证明
,证明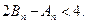
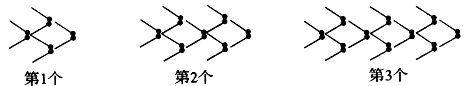
 个“金鱼”图需要火柴棒的根数为______________。
个“金鱼”图需要火柴棒的根数为______________。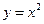 在点
在点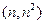 处的切线方程为
处的切线方程为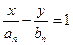 ,其中
,其中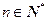
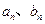 关于
关于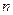 的表达式;
的表达式;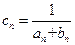 ,求证:
,求证: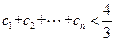 ;
;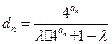 ,其中
,其中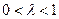 ,求证:
,求证: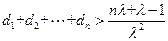
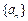 中,
中,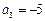 ,
,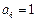 ,求此数列的通项公式;设
,求此数列的通项公式;设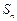 是数列
是数列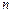 项和,求
项和,求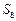 。
。