题目内容
8.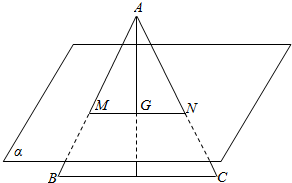 如图,在△ABC中,AB=5,AC=7,∠BAC=90°,G是△ABC的重心,过G的平面α与BC平行,AB∩α=M,AC∩α=N,则MN=$\frac{2}{3}$$\sqrt{74}$.
如图,在△ABC中,AB=5,AC=7,∠BAC=90°,G是△ABC的重心,过G的平面α与BC平行,AB∩α=M,AC∩α=N,则MN=$\frac{2}{3}$$\sqrt{74}$.
分析 利用勾股定理求出BC的长,再由BC∥平面α,得出MN∥BC,结合三角形重心的性质求出MN的值.
解答 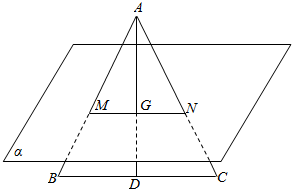 解:如图所示,
解:如图所示,
△ABC中,AB=5,AC=7,∠BAC=90°,
∴BC=$\sqrt{{5}^{2}{+7}^{2}}$=$\sqrt{74}$;
又BC∥平面α,AB∩α=M,AC∩α=N,
∴MN∥BC;
又G是△ABC的重心,
∴$\frac{MN}{BC}$=$\frac{AG}{AD}$=$\frac{2}{3}$,
∴MN=$\frac{2}{3}$BC=$\frac{2}{3}$$\sqrt{74}$.
故答案为:$\frac{2}{3}$$\sqrt{74}$.
点评 本题考查了勾股定理的应用问题,也考查了空间中的线面平行的应用问题以及三角形的重心性质的应用问题,
是基础题目.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
13.f(x0-0)与f(x0+0)的极限都存在是函数f(x)在点x0处有极限的( )
| A. | 必要条件 | B. | 充分条件 | C. | 充要条件 | D. | 无关条件 |
 如图,在长方体ABCD-A1B1C1D1中,AB=2,AD=1,AA1=1.
如图,在长方体ABCD-A1B1C1D1中,AB=2,AD=1,AA1=1. 已知椭圆T:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{3}{5}$,过右焦点F2且与x轴垂直的直线被椭圆T截得的线段长为$\frac{32}{5}$
已知椭圆T:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{3}{5}$,过右焦点F2且与x轴垂直的直线被椭圆T截得的线段长为$\frac{32}{5}$