题目内容
8.在△ABC中,已知2sinAcosB=sinC,那么△ABC一定是( )| A. | 直角三角形 | B. | 等腰直角三角形 | C. | 等腰三角形 | D. | 正三角形 |
分析 三角形的内角和为π,利用诱导公式可知sinC=sin(A+B),与已知联立,利用两角和与差的正弦即可判断△ABC的形状.
解答 解:∵在△ABC中,sinC=sin[π-(A+B)]=sin(A+B),
∴sinC=2sinAcosB?sin(A+B)=2sinAcosB,
即sinAcosB+cosAsinB=2sinAcosB,
∴sinAcosB-cosAsinB=0,
∴sin(A-B)=0,
∴A=B.
∴△ABC一定是等腰三角形.
故选:C.
点评 本题考查三角形的形状判断,考查两角和与差的正弦,利用sinC=sin(A+B)是关键,属于中档题.

练习册系列答案
相关题目
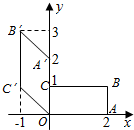 如图,矩形OABC在变换T的作用下变成了平行四边形OA′B′C′,变换T所对应的矩阵为M,矩阵N是把坐标平面上的点的横坐标伸长到原来的2倍,纵坐标伸长到原来的3倍的变换所对应的矩阵.
如图,矩形OABC在变换T的作用下变成了平行四边形OA′B′C′,变换T所对应的矩阵为M,矩阵N是把坐标平面上的点的横坐标伸长到原来的2倍,纵坐标伸长到原来的3倍的变换所对应的矩阵. 统计某学校高二年级某班40名学生的数学期中考试成绩,分数均在40分至100分之间,得到的频率分布直方图如图所示,则成绩不低于60分的人数有32.
统计某学校高二年级某班40名学生的数学期中考试成绩,分数均在40分至100分之间,得到的频率分布直方图如图所示,则成绩不低于60分的人数有32.