题目内容
13.已知向量|$\overrightarrow{a}$|=5,|$\overrightarrow{b}$|=3,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为150°,则$\overrightarrow{a}$•$\overrightarrow{b}$=$-\frac{15\sqrt{3}}{2}$.分析 直接利用向量的数量积求解即可.
解答 解:向量|$\overrightarrow{a}$|=5,|$\overrightarrow{b}$|=3,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为150°,
则$\overrightarrow{a}$•$\overrightarrow{b}$=|$\overrightarrow{a}$||$\overrightarrow{b}$|cos150°=$-\frac{15\sqrt{3}}{2}$.
故答案为:$-\frac{15\sqrt{3}}{2}$.
点评 本题考查平面斜率的数量积的运算,基本知识的考查.

练习册系列答案
相关题目
8.在△ABC中,已知2sinAcosB=sinC,那么△ABC一定是( )
| A. | 直角三角形 | B. | 等腰直角三角形 | C. | 等腰三角形 | D. | 正三角形 |
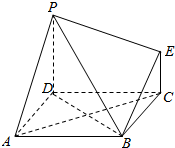 如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且
如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且