Question

【题目】函数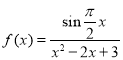，则下列结论中不正确的是（ ）

A.曲线存在对称中心B.曲线存在对称轴

C.函数的最大值为D.

Answer 1

【答案】A

【解析】

求得函数的对称轴、最值来判断BC选项的正确选，利用放缩法判断D选项的正确性，利用反证法判断A选项的结论错误.

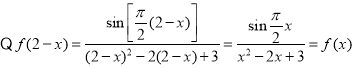，故曲线关于对称，故B正确；

由于，

当时，分母取得最小值2，此时分子刚好取得最大值1，故函数的最大值为，故C正确.

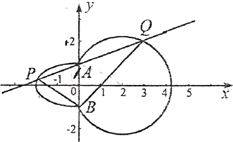
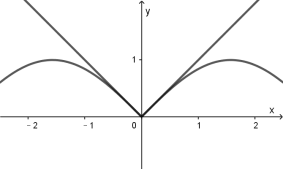
画出的图像如下图所示，由图可知.

所以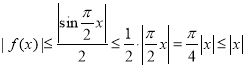，故D正确.

由于，所以不是奇函数，图像不关于原点对称.而，所以原点在函数图像上.

假设A选项正确，即存在点（为常数）是的对称中心，由上述分析可知不是原点.则原点关于的对称点为，

即①，

由于，所以在函数图像上，关于的对称点为，

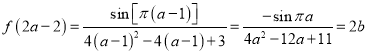即②，

由①②得，

则，

，

其判别式，方程无解.

故不存在是的对称中心，所以A选项错误.

故选：A