Question

【题目】(2015·四川）设直线l与抛物线y2=4x相交于A，B两点，与圆(x-5)2+y2=r2(r>0)相切于点M，且M为线段AB的中点.若这样的直线l恰有4条，则r的取值范围是（ ）
A.(1,3)
B.(1, 4)
C.(2,3)
D.(2,4)

Answer 1

【答案】D
【解析】显然当直线f的斜率不存在时，必有两条直线满足题设.当直线l的斜率存在时，设斜率为k .设A(x1, y1), B(x2, y2)， x1≠x2 ， M(x0, y0)， 则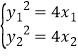,相减得（y1+y2)(y1-y2)=4(x1-x2), 由于x1≠x2 ， 所以, 即ky0=2, 圆心为C（5,0），由CM⊥AB，得k·=-1, ky0=5- x0. 所以2=5- x0 ， x0=3， 即点M必在直线x=3上将x=3代入y2=4x得y2=12, ∴-2<y0<2. 因为点M在圆(x-5)2+y2=r2(r>0)上， 所以(x0-5)2+y02=r2 ， r2=y02+4<12+4=16, 又y02+4>4(由于斜率不存在， 故y0≠0， 所以不取等号），所以4<y02+4<16, 所以2<r<4, 选D。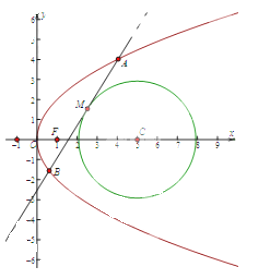

首先应结合图形进行分析.结合图形易知，只要圆的半径小于5，那么必有两条直线（即与x轴 垂直的两条切线）满足题设，因此只需直线的斜率存在时，再有两条直线满足题设即可.接下来要解决的问题是当直线的斜率存在时，圆的半径的范围是什么.涉及 直线与圆锥曲线的交点及弦的中点的问题，常常采用“点差法”.在本题中利用点差法可得，中点必在直线x=3上，由此可确定中点的纵坐标y0的范围，利用这个范围即可得到r的取值范围.