题目内容

【题目】(2015·四川）如图，四边形ABCD和ADPQ均为正方形，它们所在的平面互相垂直，动点M在线段PQ上，E、F分别为AB、BC的中点。设异面直线EM与AF所成的角为，则cos的最大值为 .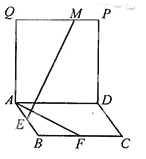

【答案】
【解析】建立坐标系如图所示.设AB=1, 则=（1，,0）， E（，0, 0), 设M（0，y, 1)(0≤y≤1), 则=（-，y, 1), 由于异面直线所成角的范围为(0, ], 所以cos==·[]2=1-, 令8y+1=t, 1≤t≤9， 则=≥， 当t=1时取等号，所以cos==≤x=, 当y=0时， 取得最大值。

【考点精析】根据题目的已知条件，利用异面直线及其所成的角的相关知识可以得到问题的答案，需要掌握异面直线所成角的求法：1、平移法：在异面直线中的一条直线中选择一特殊点，作另一条的平行线；2、补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，其目的在于容易发现两条异面直线间的关系．

练习册系列答案
相关题目

【题目】在直角坐标系xOy中，曲线C1的参数方程为 ，（其中φ为参数），曲线 ，以原点O为极点，x轴的正半轴为极轴建立极坐标系，射线l：θ=α（ρ≥0）与曲线C1 ， C2分别交于点A，B（均异于原点O）
（1）求曲线C1 ， C2的极坐标方程；
（2）当 时，求|OA|2+|OB|2的取值范围．

【题目】(2015·新课标I卷）函数f(x)=cos(x+)的部分图像如图所示，则f(x)的单调递减区间为（ ）

A.(k-,k+), kZ
B.(2k-,2k+),kZ
C.(k-,k+), kZ
D.(2k-,2k+),kZ

【题目】(2015·四川）设直线l与抛物线y2=4x相交于A，B两点，与圆(x-5)2+y2=r2(r>0)相切于点M，且M为线段AB的中点.若这样的直线l恰有4条，则r的取值范围是（ ）
A.(1,3)
B.(1, 4)
C.(2,3)
D.(2,4)

【题目】(2015·四川）已知A、B、C为△ABC的内角，tanA、tanB是关于方程x2＋px－p＋1＝0(p∈R)两个实根.
（1）求C的大小
（2）若AB＝1，AC＝，求p的值

【题目】(2015·四川）如图，A ， B ， C ， D为平面四边形ABCD的四个内角.

（1）证明：tan=
（2）若A+C=180°， AB=6， BC=3， CD=4， AD=5， 求tan+tan+tan+tan的值.

【题目】(2015·陕西）如图，椭圆E:(a>b>0)经过点A(0,-1)，且离心率为.

（1）求椭圆E的方程；
（2）经过点(1,1)，且斜率为k的直线与椭圆E交于不同两点P,Q（均异于点A），证明：直线AP与AQ的斜率之和为2.

【题目】(2015·江苏） 已知函数f(x)=x3+ax2+b(a,bR).
（1）试讨论f(x)的单调性；
（2）若b=c-a（实数c是a与无关的常数），当函数f(x)有三个不同的零点时，a的取值范围恰好是(-,-3)(1,)(,+)，求c的值.

【题目】(2015福建)已知函数=.
（1）求函数的单调递增区间；
（2）证明：当x>1时，；
（3）确定实数k的所有可能取值，使得存在，当时，恒有>．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网